Mathematics is all about patterns and critical thinking. You may be surprised to find that at least one pattern exists in whatever the concept may be.
The pattern may repeat once or several times, in an alternate manner, or by skipping tens. There are many such examples of patterns.
Counting and Number Patterns
Counting is easy if the numbers in a set or pattern are only differentiated by 1. The challenge is when the patterns utilize more than one way in it to arrive at an answer.
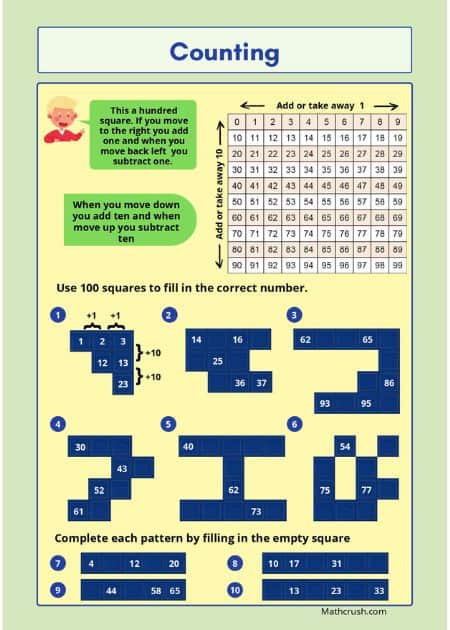
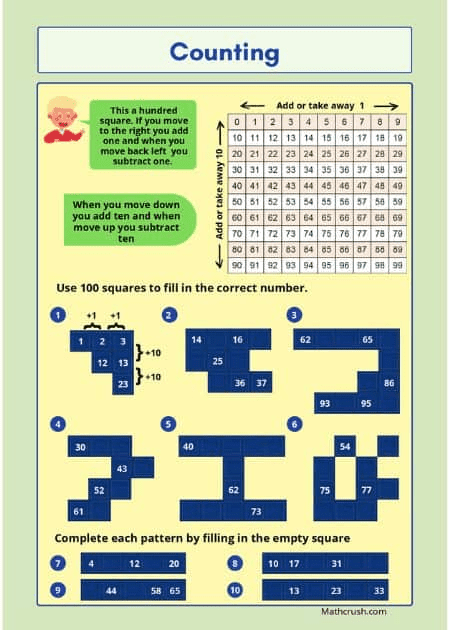
Primarily, a counting box is used to learn all about the basic patterns. It has 10 vertical columns and 10 horizontal rows.
Along a row, the pattern is, 1 is to be added when moving from one number to another. For example, if you begin with 0, add 1, and the resulting number in the next box will be 1.
Similarly to that 1, add 1, and the resulting number in the next box will be 2. In this way, the pattern moves forward until the final box has the number 9
Along a column, the pattern is, 10 is to be added when moving from one number to another. For example, if you begin with 0, add 10, and the resulting number in the next box will be 10.
Similarly to that 10, add 10, and the resulting number in the next box will be 20. In this way, the pattern moves downwards until the final box has the number 90.
The end box number of each row or column differs. In the vertical column, the difference is 10, and the pattern goes 9, 19, 29……. In the horizontal row, the difference is 1, and the pattern goes 90, 91, 92…..
The patterns are not restricted to any specific numerical value or shape. They keep on changing, and so does their base pattern.
To solve any kind of pattern, irrespective of shape, all you have to find out is the foundational rule of the set, and the pattern will reveal itself before you in no time.
The main aim of utilizing patterns is it helps the student develop critical or lateral thinking. It expands the narrowed vision of students, and a much broader spectrum enables them to formulate solutions on their own in a unique way.
The below page mini-packet covers basic counting and number patterns. It uses puzzles to help students better understand numbers and their patterns.
Key concept: Counting and understanding number patterns are crucial concepts that all students need to master and can save them time as mathematics becomes more difficult.

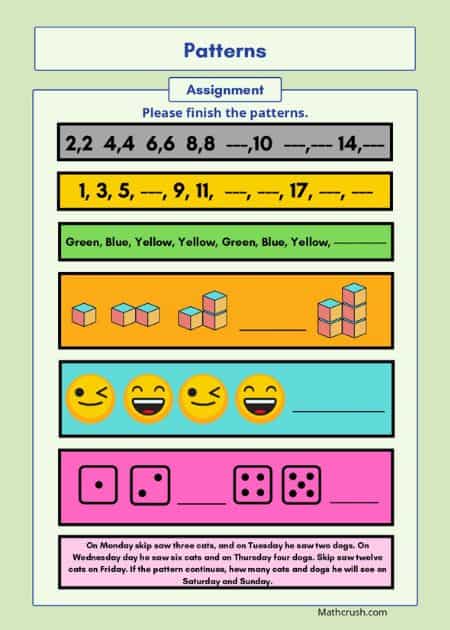
Patterns
| The Below worksheets introduce patterns. Students complete the patterns for each problem. The problems consist of numbers, objects, and one word problem. |

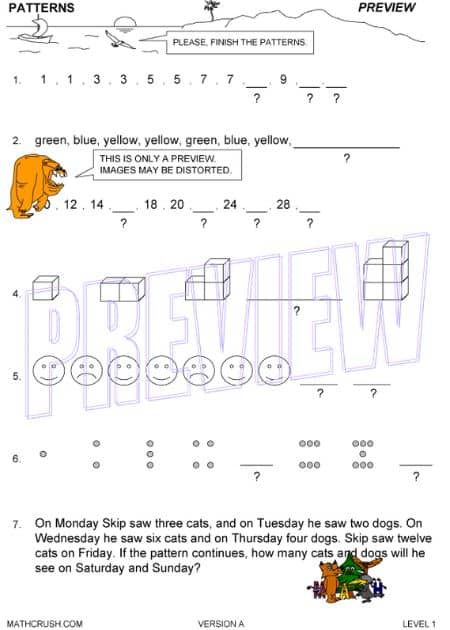
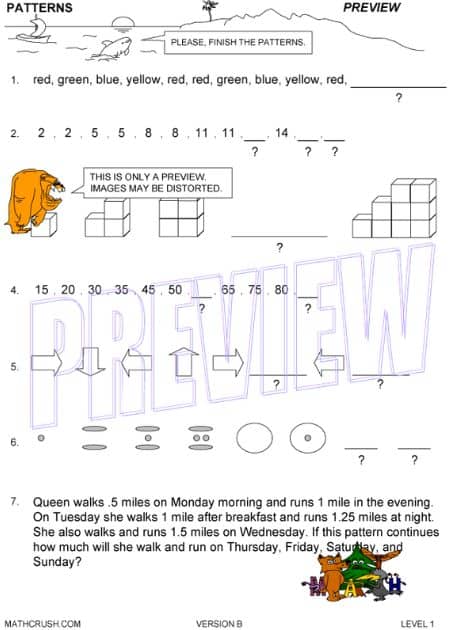
Pattern Puzzles – Level 1
The below worksheets has students determine the missing values of three different puzzles. Students need to find the pattern and then calculate the missing amounts.
Key concept: Mathematics is filled with patterns. The better students are at seeing them the faster they get at solving problems.


Numerical Puzzles – Level 1
The below worksheets includes math puzzles.


Patterns and Puzzles (B) – Level 2
The below worksheets has three different puzzles for students to recognize
patterns.
Key concept: Puzzle and Pattern problems help students think of alternative solutions and solve more complex problems.


Math Puzzles – Numbers Level 2
The below worksheets has students solve various puzzles. They either determine the missing values or find the number that does not belong in a group.
Key concept: Patterns and puzzles are a great alternative to helping students gain confidence in solving problems.

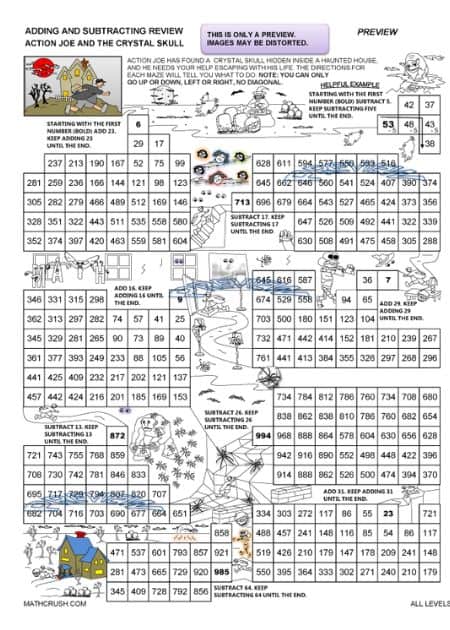
Adding and Subtracting Review All Levels
The below worksheet is designed to help students review addition and subtraction. Students add or subtract a certain number and follow the pattern until helping Action Joe escape.

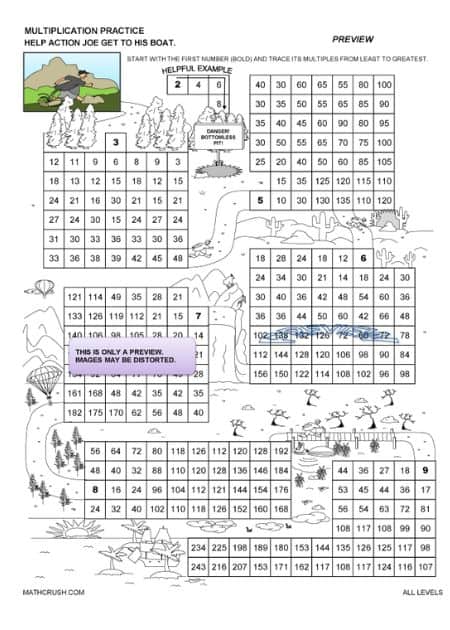
Multiples / Multiplication Practice – All Levels
The below worksheet reviews multiples to help students with their multiplication. Students find the multiples from least to greatest in each maze to help Action Joe.

Multiplying and Dividing Review-All Levels
The below worksheet is designed to help students review multiplication and division. Students multiply and divide a certain number and follow the pattern until helping Action Joe find the treasure


Mixed Review – All Levels
The below worksheets is designed to help students with basic review. Vocabulary covered: least, greatest, multiples, divisible, prime numbers, perfect square, odd, and even. Another adventure for Action Joe.


Algebraic Operations Puzzles
The various Algebraic Operations of Division, Multiplication, Addition, and Subtraction are part of the pattern formation. It is not so that only one type of operation is part of one pattern.
The problem may exhibit multiple operational incorporations in numerous patterns. The complexity only increases from here; there is no step back to the pattern we studied earlier.
It is also possible that patterns may not only run linearly. They may be backward and diagonally too, and this is precisely what patterns make the students comprehend that there is immense space for alternative solutions.
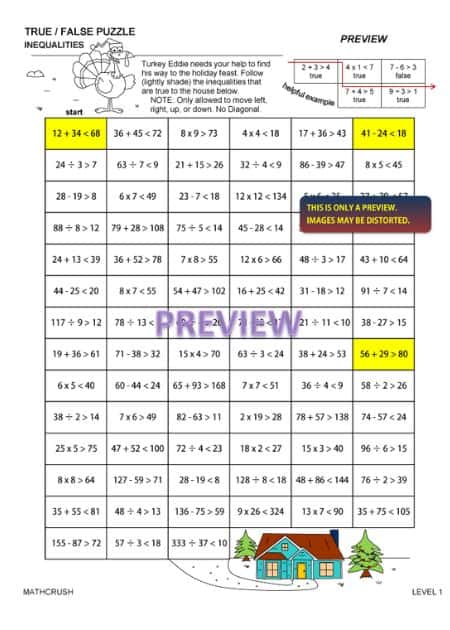
Inequality Puzzles
These are again a subpart of the Operational Puzzles. Instead of the usual arithmetic operations in equations and expressions, these have a greater than and lesser than symbols.
Although this is the case, the key is still the same to unlock them. Figure out the pattern, and you can understand how the expression has been created.
One clue is, there is one false expression between two true ones. So start by eliminating the false ones, and you will have the true ones appearing.
This maze worksheet reviews inequalities. Students find the true statements and follow them to help Turkey Eddie get to his feast.
Helpful hint: The maze might look big but if student’s think about it, certain problems can be eliminated because they are between
two true statements.
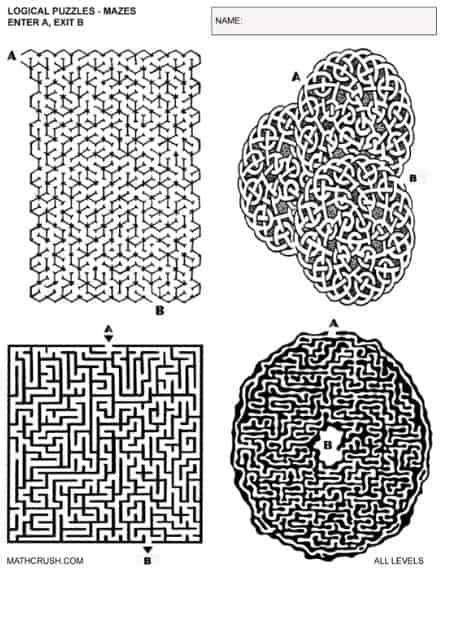
Logical Puzzles (Mazes) – All Levels
The below worksheet has four different mazes to challenge your students.
Key concept: Puzzle and Pattern problems help students think of alternative solutions, especially working backwards. You might be surprised who finishes each maze first.

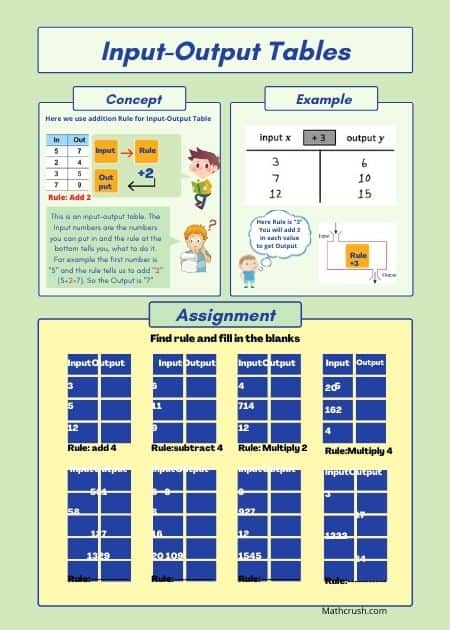
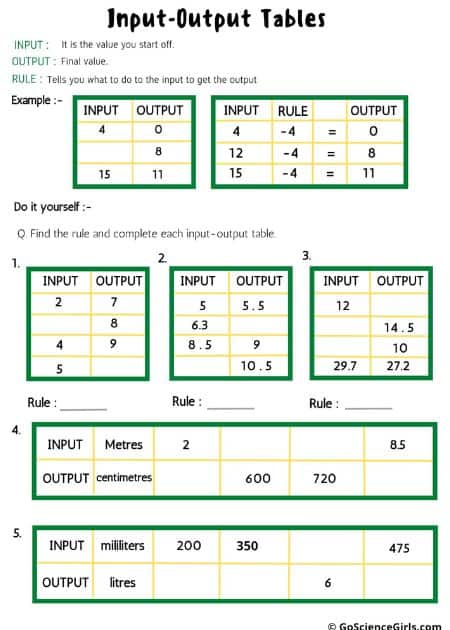
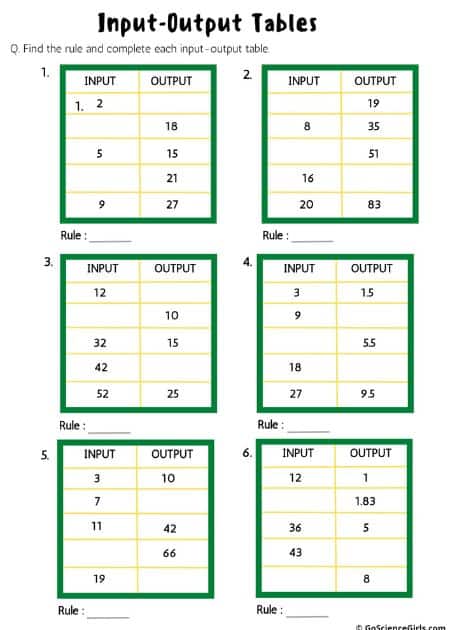
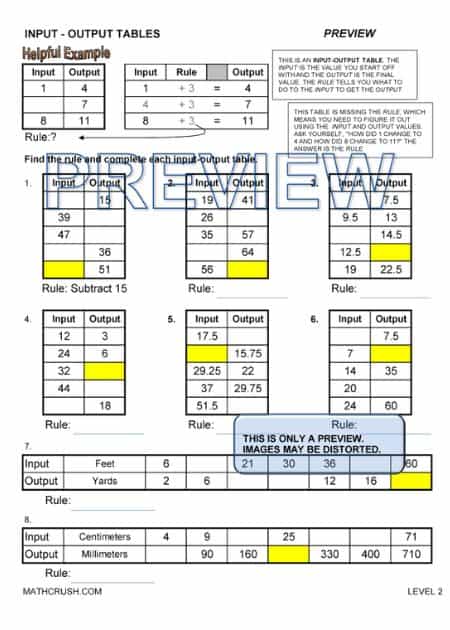
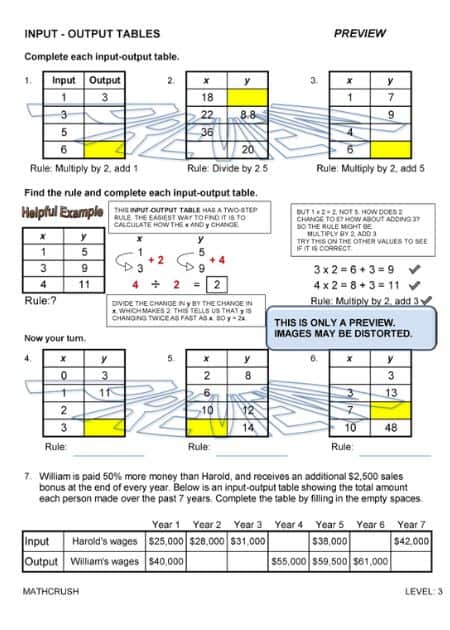
Input-Output Tables
In these types of tables, the pattern is to figure out the number of additions, how many times multiplication occurs, whether the denominator is greater than the numerator in divisions, and subtracting gives negative or positive integers.
If the given input values are – 45, 51, 62, and 75, and the output values of first and third are 47 and 64, then you can guess the rule to be ‘Add 2’. And so, the output values will be for the second and fourth will be 53 and 77.
These one page worksheets cover input-output tables. Students need to find the rules and complete the tables. Input-output tables help students recognize patterns and build a relationship between lines and equations. There is a different worksheet for each level.

Multiplication and Geometry Game
Activity excites students, and it is thus the best way to explain new and complex concepts. You can also teach patterns with the help of these Multiplication and Geometric Games.
A sheet containing many boxes, each with two statements, should be printed and cut into respective boxes. One statement is an expression with ‘I have,’ and another with ‘Who has.’ Both expressions are different and unrelated to each other
Best as a group activity, you should distribute these chits to all the students. Each student should then loudly read both the expressions with their headings of ‘Who has’ and ‘I have.’
The students must then figure out whether they have either of the statements read aloud by the said student. If they do, they should respond with the correct expression to the expressions in question.
These games will improve their hunger for competition, and a bonus will be their perfect grasp of the lesson. Also, they will understand some unconventional ways, where there is more than one answer to a question.
An Example from the Geometry Game: A square can be a rhombus, but a rhombus is not a square. These types of conclusions cannot be arrived upon by simply going through the lesson. The students need to use their critical thinking skills.
The below worksheet describes about the gam


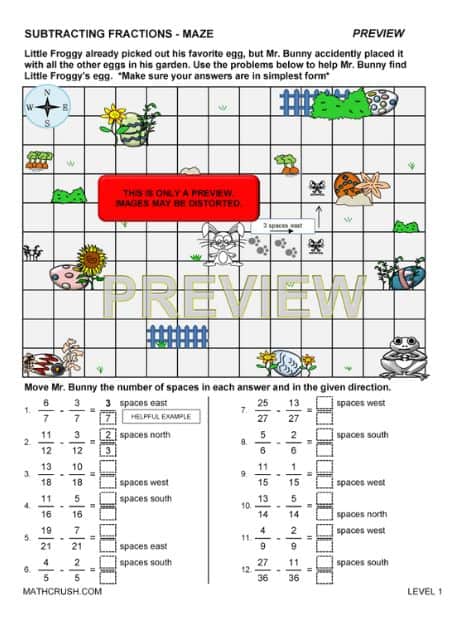
Subtracting Fractions
There are normal fractions, and then there are mixed fractions that first need to be converted to normal functions to move forward with subtracting.
To do that, multiply the denominator with the left whole number and add to it the numerator value. The answer you get will be the normal numerator, and the denominator will remain the same.
If there are no mixed fractions in the expression to be solved, you can directly begin from the following step of multiplication.
For the subtracting part, cross multiply the denominators with the numerators of the opposite terms and with the denominators too. This will give a common denominator.
However, in the numerator, the multiplied answers are separated by the algebraic function: subtraction. Subtract the numerators, and there you have the final fraction answer.
The below maze worksheets have students answer subtracting fraction problems and then use the answers in the numerator or dinominator to move Mr. Bunny in the stated direction to find the missing egg. There is a different worksheet for each level.




Area Puzzles
Ever imagined measuring something without using a ruler? No? With this concept of Area Puzzles, you can measure the different lengths of the unnamed shape or quadrilateral using the given data itself.
The values of the areas given of the smaller boxes are nothing but the squares of their sides. This way, you will get the measurement of sides of the adjacent squares, and you can ultimately reach the box whose area actually needs to be calculated.
These puzzles also follow the principle of patterns and critical thinking.
The below worksheets is an area puzzle where students try to determine if the quadrilateral
is a square or not. They need to use the given information to find the sides of the other smaller squares inside the shape and then use that information to determine the length and width of the larger quadrilateral.


Battleship
Use the concepts of Coordinate Algebra in playing this game. All rules, points, coordinates must be adhered to when the game is in progress.

Who Done It?
Use the concepts of Time and Money to figure out the robbery. Carefully read the timings, money bills, and any other such data while processing the solution.
The below worksheet has students use their basic math skills to solve a robbery. They read the information and look at the pictures to figure out who committed the crime.

Who is Who?
This requires logic and reasoning. The students learn to differentiate between which are the factual statements and which are the false ones.
Critical thinking and pattern figuring are the way to go about this.



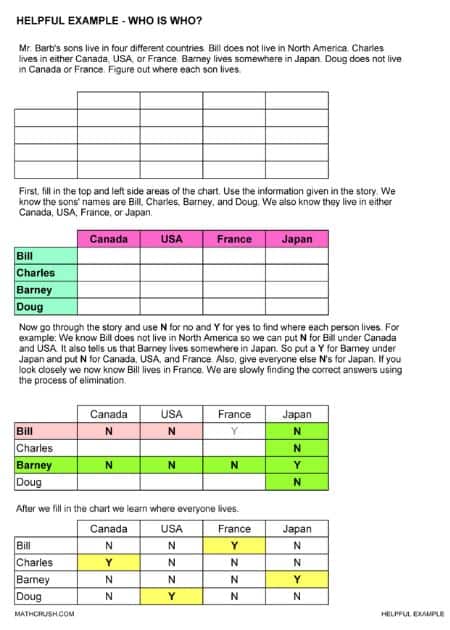
Who is Who? Soccer – Level 3
The below word problem worksheet has students put together information and solve simple problems to organize details about a soccer (football) team.

Math Vocabulary
To solve this, you will need to understand and learn different concepts’ definitions, key terms, and alternate names. Beginning with types of numbers, continuing with decimals, fractions, exponents, and towards the end, graphs, mid-point, etc.
One common misconception among the majority of the students is, they equalize Factors and Multiples. Let us give a once over to them.
Factors are exact divisible numbers to the one in question, without leaving any remainder. These are less in number compared to Multiples.
Multiples are the results of multiplying a number with another number. Both the two multiplying numbers are the factors of the result, which is the Multiple.
Multiples have factors. The reverse is also possible but rare in occurrence.
Example: 5 x 4 = 20
Here,
5 and 4 are factors of 20.
20 is the multiple of 5 and 4
The below worksheet helps students practice basic math vocabulary. It can be used as a single worksheet or separated into two smaller ones and used as warm ups.

Critical Thinking – Multiplication Level 1
The below worksheets is on multiplication. Students use two sets of 0-9 numbers to
fill in the empty boxes. They look at each picture and use their basic multiplication skills to answer the number of each item.


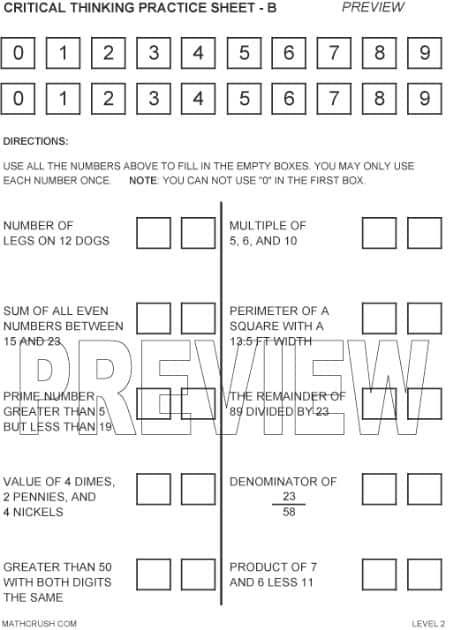
Critical Thinking A – Level 2
The below worksheet is on math terminology. Students use two sets of 0-9 numbers to
fill in the empty boxes. They need to use their basic math vocabulary and thinking process to answer the questions correctly.
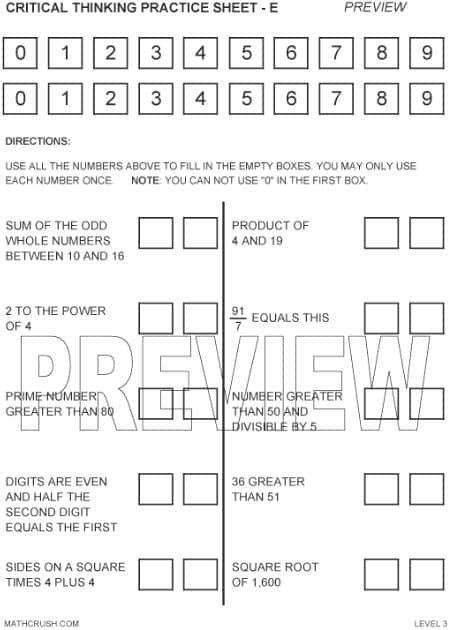
Critical Thinking C – Level 2
The belo worksheet is on math terminology. Students use two sets of 0-9 numbers to
fill in the empty boxes. They need to use their basic math vocabulary and thinking process to answer the questions correctly.
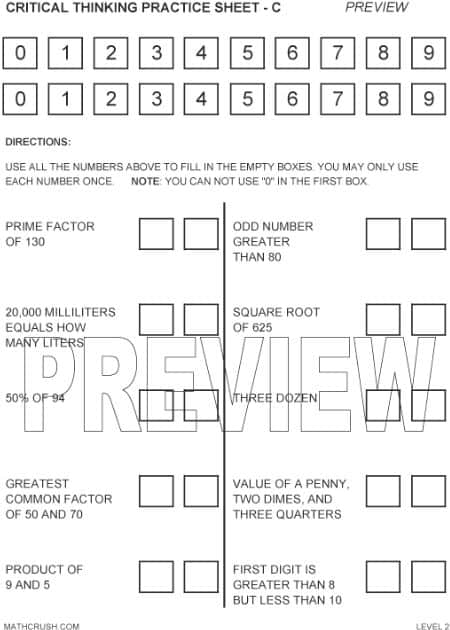
Critical Thinking D – Level 3
The below worksheet is on math terminology. Students use two sets of 0-9 numbers to
fill in the empty boxes. They need to use their basic math vocabulary and thinking process to answer the questions correctly.
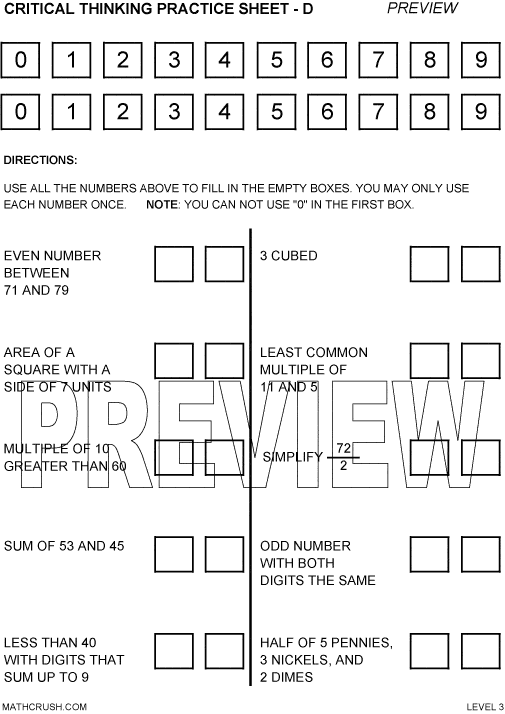
Critical Thinking E – Level 3
The below worksheet is on math terminology. Students use two sets of 0-9 numbers to
fill in the empty boxes. They need to use their basic math vocabulary and thinking process to answer the questions correctly.
Variable and Substitution Puzzles
Use the concepts of Variables and Substitutions as studied earlier, and solve the puzzles.
Variable Puzzles – Level 1
The below worksheets use puzzles to help kids practice their algebra skills. Students are given five variables (letters) and have to find what numbers they represent. They are given equations as clues and a grid to help solve the unknown variables. This can also be used to practice the
process of elimination for test taking skills.



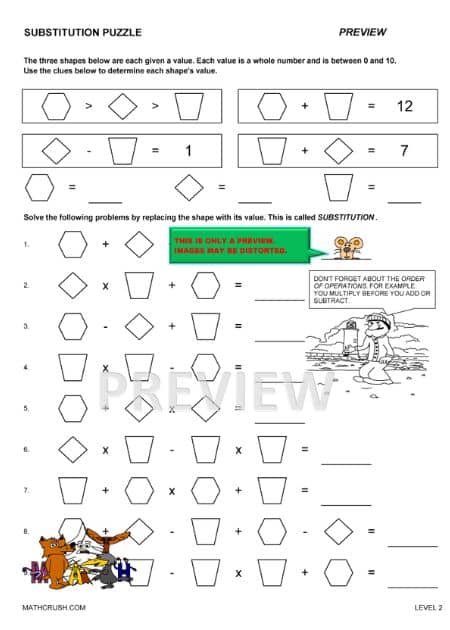
Substitution Puzzle – Level 2
The below worksheet has students determine the value of three shapes and then substitute the values into expressions. It also reviews the order of operations.
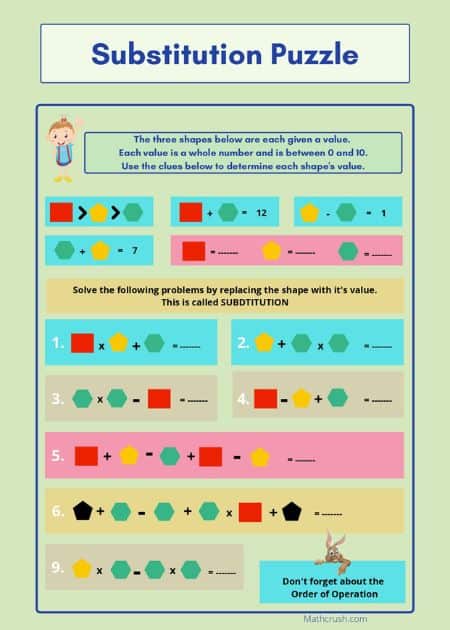
Mean, Median, Mode, and Range Puzzles
Use the concepts of Mean, Median, Mode, and Range to solve the respective puzzles. Apply practically in recognizing the patterns.
The below worksheet help students practice mean, median, mode, and range. Students need to calculate the missing cards based on the given clues.


Crossmath Puzzles
These refer to using the different Algebraic Operations in the combination of twos. As in a crossword puzzle, the more you solve the clues, the easier it is to find the remaining words; similar is the case with solving these crossmath puzzles.
Begin by using one-digit numbers in multiplication to similar numbers. Use your tables to try /the trial and error method and fill in the boxes.
Crossmath Puzzle – Level 1
The below worksheets is similar to a crossword puzzle. The goal is to fill in the empty
spaces using the arithmetic to get the answers at the bottom and right column. Each puzzle has a set of numbers that can only be used once.Addition and Subtraction.


Help page for crossmath puzzle
Crossmath Puzzle – Level 2
The below worksheets is similar to a crossword puzzle. The goal is to fill in the empty
spaces using the arithmetic to get the answers at the bottom and right column. Each puzzle has a set of numbers that can only be used once. Addition and Subtraction.



Help page for crossmath puzzle
Crossmath Puzzle – Level 3
The below worksheet is similar to a crossword puzzle. The goal is to fill in the empty
spaces using the arithmetic to get the answers at the bottom and right column. Each puzzle has a set of numbers that can only be used once. Multiplication and Division.
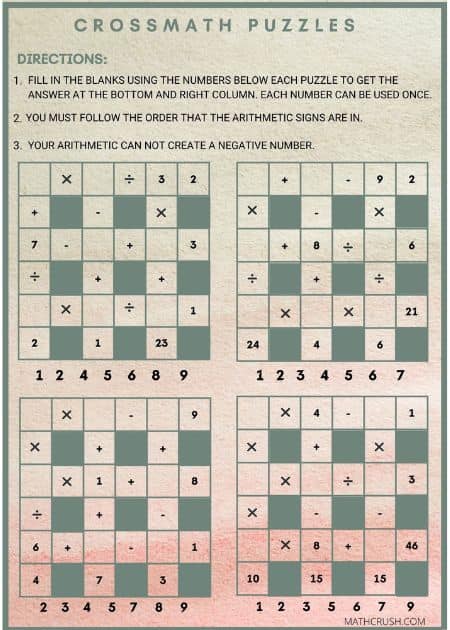

Help page for crossmath puzzle
Crossmath Puzzle – Level 4
The below worksheet is similar to a crossword puzzle. The goal is to fill in the empty
spaces using the arithmetic to get the answers at the bottom and right column. Each puzzle has a set of numbers that can only be used once. Multiplication and Division.

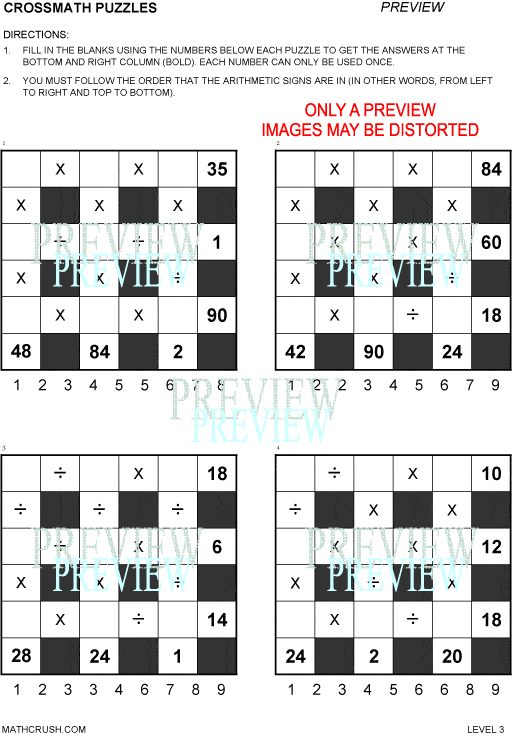
Help page for crossmath puzzle
Crossmath Puzzle – Level 5
The below worksheet is similar to a crossword puzzle. The goal is to fill in the empty
spaces using the arithmetic to get the answers at the bottom and right column. Each puzzle has a set of numbers that can only be used once. Multiplication and Division.
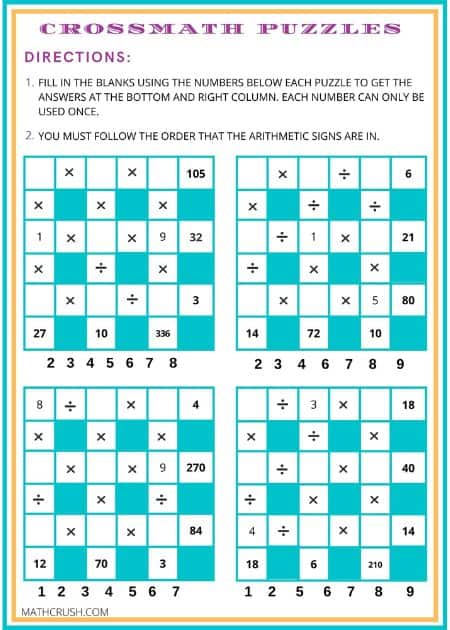


Help page for crossmath puzzle
Enquiry Learning
This refers to understanding a concept based on one’s conclusions regarding the various algebraic expressions. There is no one true answer.
The possibilities are many, but you need to explain how and why you arrived at a particular conclusion for each word problem. Verbal Expressions are more prominently found, so understand and comprehend what the questioner is asking you.
Gather data, explore different possibilities. Finally, select the aptest one and suited to be the solution to the particular question.
The below worksheets has enquiry learning problems. Each question could have multiple
solutions, but the students are expected to show how they came up with their conclusions.

Enquiry Learning – Probability
The below worksheet has three enquiry learning problems. Each probability question could have
multiple solutions, but the students are expected to show how they came up with their conclusions.

Sampling
Situations are unpredictable, and out of them, you need to make a good sample and best inferences by using critical thinking. Data is crucial to this.
The best output, along with the merits and demerits, gives a sample substance and the fuel to move it further. If you fail to think exponentially, meaning out of the ordinary, the chances of your solution matching with others increases, making your sample difficult to be accepted.
The below worksheet covers sampling. It includes word problems that ask students to examine samples, show whether or not it fairly represents the entire population, and think about how certain samples can produce better inferences.

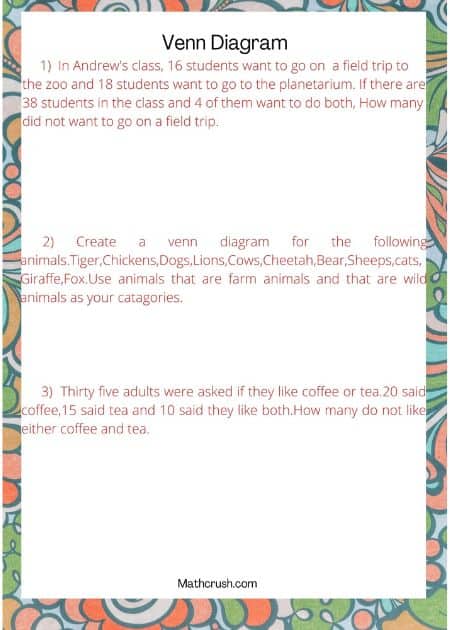
Venn Diagrams
Repetition does not always work. Rather than writing stuff twice, you can find the similarities and dissimilarities among the data and create a diagram pointing out those with focus.
These diagrams are called ‘Venn Diagrams,’ and these are circular.
If there are three things in comparison and there is a resemblance, then the three shapes overlap each other. The likes are then mentioned in the overlapping part representing that the highlighted part depicts the qualities common to the three in comparison.
If there are only two comparable quantities, the method used is the same.
Differentials are written in the respective circles, parts that do not overlap with the adjacent circles.
The below worksheets introduces Venn diagrams. Students use Venn diagrams to show the relationship between two sets of information.



Critical Thinking Help Packets
Counting and Number Patterns-Level 2
The below worksheet covers basic counting and number patterns. It uses puzzles to help students better understand numbers and their patterns.

Venn Diagrams – Level 1
The below worksheet introduces Venn Diagrams. Students learn to use pictures (circles) to help
represent sets and show how they are related.


Conclusion
Critical thinking in mathematics, especially in Algebraic Concepts, is crucial to expand further your knowledge and understanding of all concepts relating to it.
If you do not stretch your mental capacity far wide and develop the skill of multilateral thinking, then the chances of excelling at Algebra lessen significantly.
