These home-grown worksheets were created to walk kids through finding the Mean, Median & Mode process.
In these worksheets, we focus on exploring mean, mode, and median compared to each other. This is done by having students compare the data from three different sets of numbers to each other.
Understanding Mean, Median & Mode
Mathematical concepts of mean, median, and mode are called ‘Measures of Centre.’ Why? Because they more or less, i.e., slight differences, give the middle, center, or medium of data collected.
Data of any type needs specific markers to keep as bookmarkers to understand certain characteristics, probabilities, and frequencies. With Mean, Median and Mode, you have the extra aid in configuring the repetitions of each type of data.
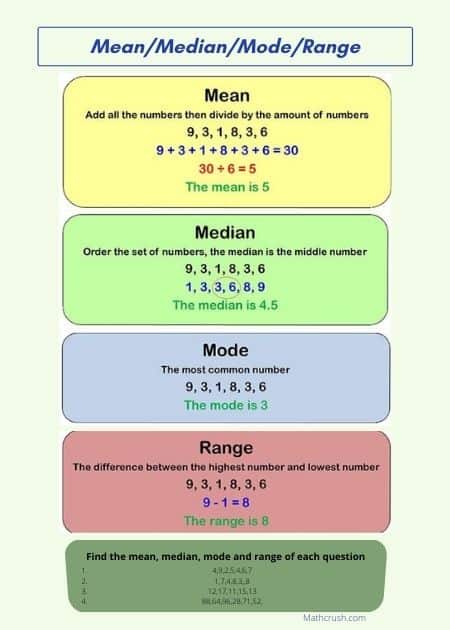
Mean
Supposing you have a large set of numbers and you do not know the ‘average’ value of the entire set. What do you do?
Mean is defined as that ‘average’ or a rough figure of the representing set. It gives a middle value of what the data consists of.
Example: A set has the following numbers – 13, 57, 39, 90, 2, 44, 9, 34, 56, 95. What is the mean value?
Method:
To calculate the mean, you will have to first node down two things. They are –
- Sum of all the terms
- Number of total terms
So, from the above set,
- Sum of all the terms = 13 + 57 + 39 + 90 + 2 + 44 + 9 + 34 + 52 + 100 = 440
- Number of total terms = 10
The formula for calculating Mean is –
Mean = Sum of all the terms / Number of total terms
= 440/10
= 44
Median
Median defines the middle value of the representing set. But first, to determine that, you will need to arrange the set in increasing order of numbers.
Arranging the numbers from lowest to highest numbers makes it easier to point out the central number. To do that, start counting the terms from both the ends, the right, and the left, simultaneously.
Once you reach the midway mark, the number at the center is your Median.
Example: Find out the median value,
- If the set has odd number of terms: 13, 57, 39, 82, 2, 21, 44, 9, 34, 56, 90
- If the set has even number of terms: 13, 57, 39, 82, 2, 44, 9, 34, 56, 90
Method:
- Simultaneously count the terms, beginning from 13 on the left side and 90 on the right side. In the middle, you will find that 21 is left out, and so 21 is the median value of that set.
- Simultaneously count the terms, beginning from 13 on the left side and 90 on the right side. But, since this is an even number set, you will find two middle numbers instead of one middle term.
In such a case, simply add the two numbers to get your median value. In this set, those two numbers are 2 and 44, on the addition of which we get 46 as the median value.
Mode
It is more than probable that you have a term that repeats itself once, twice, thrice, or even more times in each set. From the repeating terms, the term with the most repetition is called Mode.
It basically represents the ‘most’ out of the set.
Example: The given set is – 13, 57, 13, 90, 21, 21, 13, 9, 34, 56, 100. What is the mode of this set?
Method: Begin counting the terms that are repeated the most. Here, 21 and 13 are the two repeating terms.
However, from 21 and 13, the former is repeated 2 times, while the latter is repeated 3 times. So, 13 precedes 21 for the position of Mode.
Range
A different yet related concept of Mean, Median, and Mode is the Range. It is a simple subtraction between the largest and the smallest number among the set.
The Range gives us the understanding of the least and most values crucial to analyzing particular logistics.
Example: 13, 57, 39, 90, 2, 21, 44, 9, 34, 56, 100 is the set of terms before you. Find out the Range.
Method: Read all the numbers once, and check the highest and lowest numbers twice before noting them down. Data from the above set gives 100 as the highest value and 2 as the lowest.
The formula for calculating Range is –
Range = Highest value term – Lowest value term
= 100 – 2
= 98
Note: It is possible to have the same value term as the answer for Mean, Median, Mode, and Range. An example set would be 3, 4, 5, 5, 8.
Mean, Median, and Mode –Worksheets
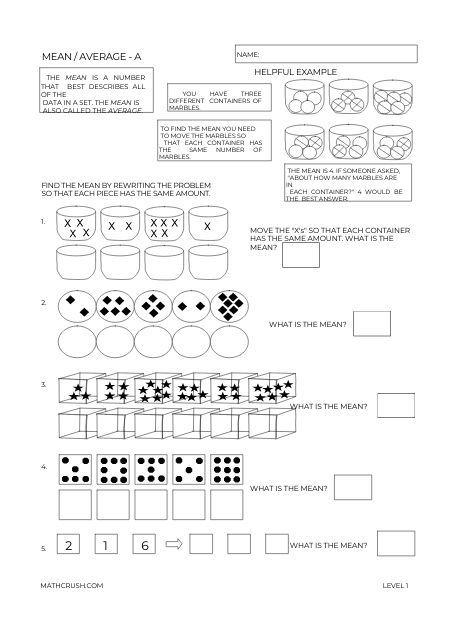
Finding Mean Worksheet – Level 1
The below worksheet introduces mean. The first page uses a more visual concept to
explain what the mean or average is. The second page uses the basic expression of adding and then dividing.

Median, Mode, and Range Worksheet – Level 1
The below worksheet covers median, mode, and range. It only shows students how to find the answers not what they truly represent.


Mean, Median, Mode, and Range Worksheet – Level 2
The below worksheet covers mean, median, mode, and range. It includes more difficult
problems for the median and mode, and introduces the best time to use each measure of central tendency.


Mean, Median, Mode, Range Worksheet – Level 2
The below HOLIDAY art worksheet reviews mean, median, mode, and range. Students answer the problems, and then find and color the turkey that matches each answer.


Mean, Median, Mode, Range Puzzles Worksheet – Level 2
These one page puzzles help students practice mean, median, mode, and range. Students need to calculate the missing cards based on the given clues.


Answer, Find, and Shade (2 in 1)
Mean, Median, Mode, and Range Level 2
The below art worksheet has two pictures hidden inside. Students will need to find the mean, median, mode, and range for each set. They must answer all the questions but get to choose to only shade in the odd numbered or even numbered problems to get one of the two different pictures.

Test Review Word Problems
Average, Proportions, and Unit Rate
The below worksheet is designed to help students prepare for multiple choice test questions. It covers average, proportions, and unit rate. It is designed for students in grade 5 or year 6, but can be used for any students studying these topics.

To Conclude
The mathematical concepts of mean, median, and mode are majorly used in the Analytics department of various corporations and industries to make graphs and charts relaying statistic
al information.
This information is then used to make any changes and improve the results, making them more beneficial for our usage.
