Order of operations worksheets are an incredibly helpful learning tool for students, especially if they need to learn more about order of operations.
Students can practice their skills by following the steps on these free printable worksheets. Teachers can also use these worksheets as part of their lesson plans.
Order of Operations Worksheets
Free Worksheets on Order of Operations (Level-1)
Order of operations is a great way of solving mathematical expressions that involve multi operations like addition, division, multiplication, exponents, etc. The primary school students follow either the PEMDAS or BODMAS rule of order of operation to simplify the multi-operation math problems. The worksheets included here cover all the four basic math operations using whole numbers, fractions, and decimals.
Learning Tip: Take an example like 4 + 8 x 2; simplify this simple math expression in two different ways and check your answers. The answers will vary and the result which comes after following the order of operations is the correct answer.


Free Worksheets on Order of Operations (Level-2)
PEMDAS or BODMAS rules reflect the order of steps that revolve around the four major math operations to simplify the math expressions. The worksheets on the order of operations at level 2 include various questions that cover advanced-level math operations like parentheses. Practicing these worksheets is a standard approach for students to excel in simplifying math operations.

Free Worksheets on Order of Operations—Free Samples (Level-2)
The free sample of worksheets on order of operations provides stepwise instructions that make students familiarize themselves with the order of operations. Also, these worksheets provide questions in different versions with different levels of difficulty. Students need to pick the questions based on their requirements and level of difficulty interested.
Misinterpretation of Students: Students need to remember that multiplication and division take the equal role and are performed either before or after one another. In the same way, addition and subtraction also take an equal role in the order of operations. However, whenever we do a math calculation, do remember to perform these four basic operators from left to right.

Free Worksheets on Order of Operations (Level-3)
Many activities in real life involve multi-operation math calculations! So, we require some pre-requisite familiarity on simplifying such multi-operation calculations. Explore these worksheets that provide you good practice for performing complex math expressions easily and simply. In addition, these worksheets cover exponents, parentheses, apart from the other four operations.

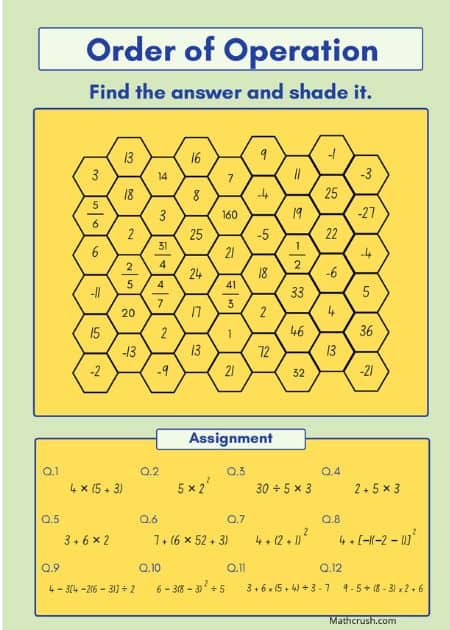
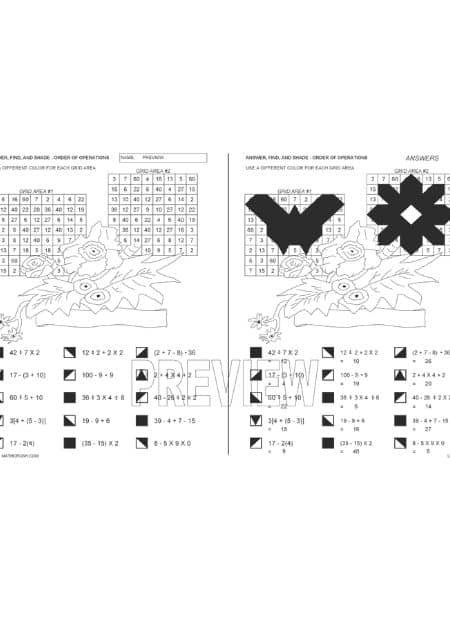
Order of Operations Worksheets using Find and Shading Skills (Level 2)
Students use practice handouts that reveal the set of the order of operation rules to simplify a math expression in a fun way. Shading the answers in the worksheets provides great practice, which helps them to easily clear their term exams in the school. These worksheets are nothing but art pages and are highly useful for making special occasions like Mother’s Day and Thanks Giving educational.
Misinterpretation of Teachers: The phrase “Please Excuse My Dear Aunt Sally,” is commonly used by the teachers to teach the shortcuts of the order of operations. It is a good idea of learning but many students misinterpret that multiplication comes before the division and addition come before subtraction. Multiplication and division play equal role, as well as addition and subtraction, plays a similar role in the order of operations.
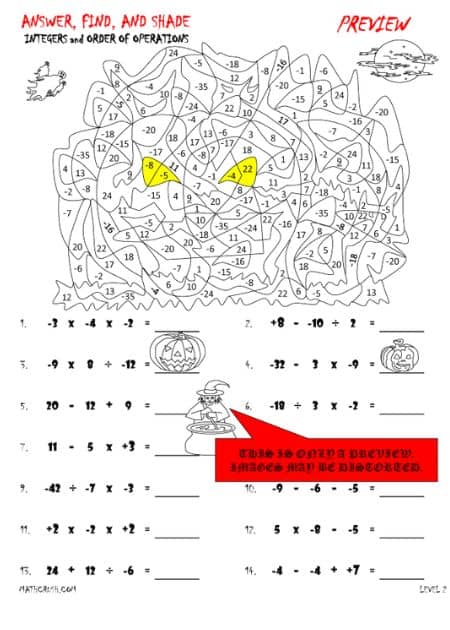
Worksheets on Order of Operations using Integers (Level 2)
Integers are the whole numbers meant for any sort of math calculations and are never exist in decimals. Learning the order of operations using integers offers a great introduction for students to excel in the concepts of integers and order of operations.
The worksheets provided here add up extra spice to your learning with positive and negative numbers and are suitable for primary grade students. Great for Halloween events to engage children of kindergarten and elementary grades!
Key Concepts: Students understand the difference between whole numbers and fractional numbers using the order of operations.

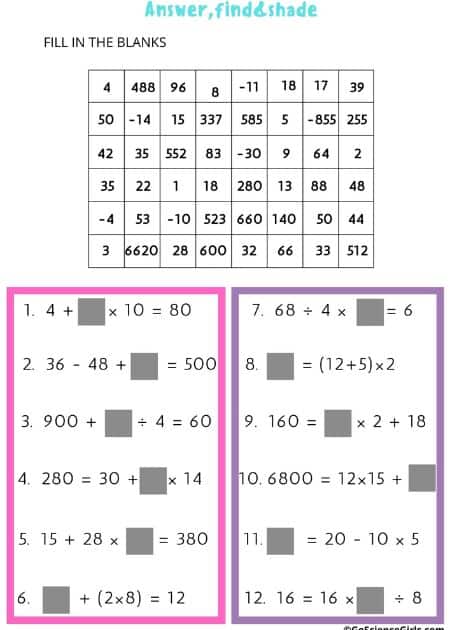
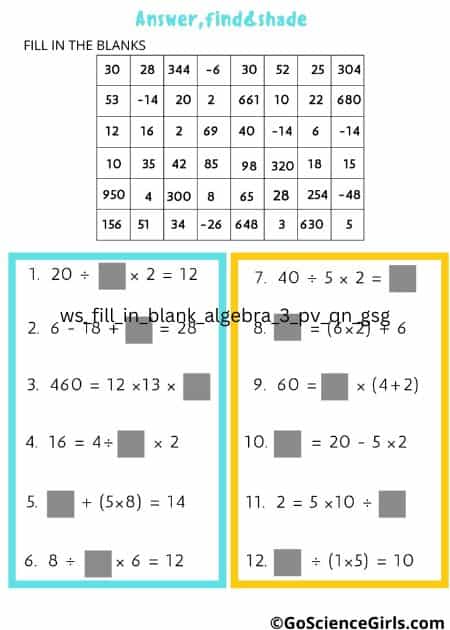
Fill in the Blank Worksheets to Practice Order of Operations (Answer Colour Find)
Practicing fill-in-the-blank worksheets are interactive and help students to solve various math equations by reviewing the basic order of operations.
Learning Tip: Let the students turn their worksheets into the artwork by shading the answers using different colors of their choice.

Fill in the Blank Worksheets to Practice Order of Operations (Answer Shade Find)—2
Students can find different questions on the order of operations for different grades in these fill-in-the-blank worksheets. Fill in the blanks allow them to learn basic math operators using detailed skills like exponents and parentheses. Drawing and shading the answers support student’s artistic skills, which helps them to find the solutions using current learning skills.
Learning Tip: Students can check out the pictures to figure out the solution patterns. If they find the shape incorrect, then they need to resolve the problem to figure out the correct pattern.




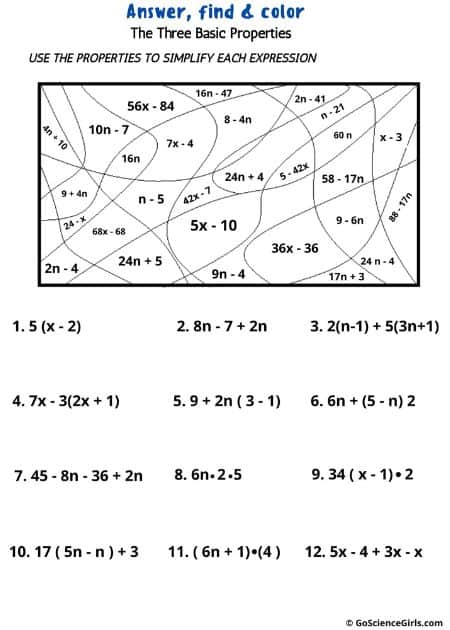
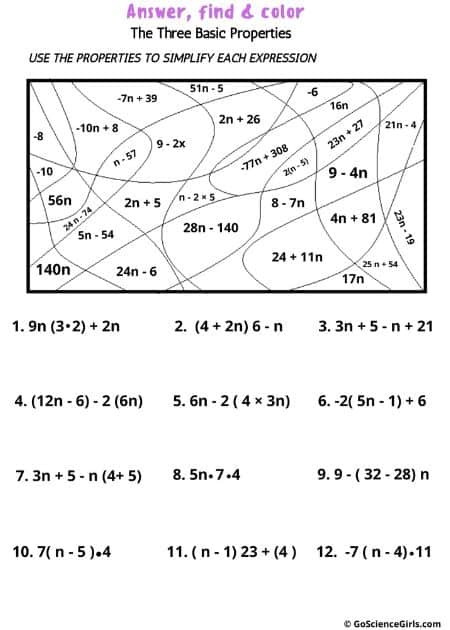
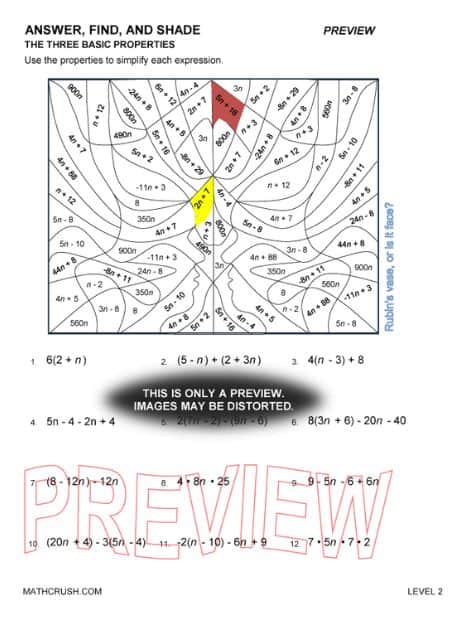
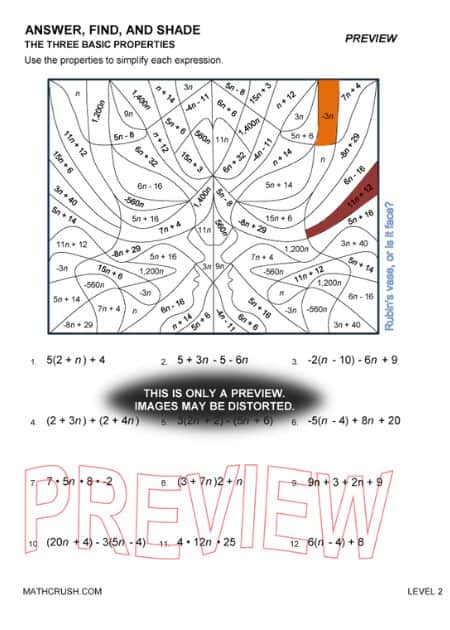
Worksheets of Basic Properties of Numbers (Level-2)
Associative, Distributive, and Commutative are the three basic properties of numbers that reveal the advanced math operations to higher grade students. The worksheets involve different questions and activities, which are great practice for advanced maths such as algebra.
Substitution Numbers Worksheets (Level-1)
Substitution numbers play a significant role in mastering students in solving complex algebraic expressions in maths. The substitution worksheets are a great resource to learn about substitution numbers and convert them into magic squares, negative numbers, etc.
Misinterpretation of Substitution: Do not misinterpret the expression 4xy, where x = 4 and y = 5; 4xy = 4 x 4 x 5 with 4xy = 445.


Substitution Numbers Worksheets (Level-2)
The worksheets on substitution numbers consist of the medium-level degree of difficult questions that cover fundamental math values into algebraic expressions. In addition, these worksheets are great for practicing substitution numbers using multiplication and division operators.
Key Impressions: Students need to be aware of different variables and expressions that define substitution numbers.




Substitution Numbers Worksheets (Level-3)
Algebraic expressions are highly useful in any field like science, computing, and healthcare. To simplify any sort of algebraic equation, the substitution concept is a powerful tool for students. On the other hand, practicing the worksheets on substitution numbers make them substitution experts.
Important Note: If the students become substitution experts, they can solve math equations using the order of operations.




Worksheets on Substitution (Answer Find and Shade Level-1)
The answer, find and shade method makes these worksheets an art worksheet that reviews substitution numbers that simplify complex algebraic equations.
Student Misinterpretation: Consider r, y and z are the variables and when these variables are placed side-by-side or each other, it refers to multiplication. So, XYZ = X x Y x Z
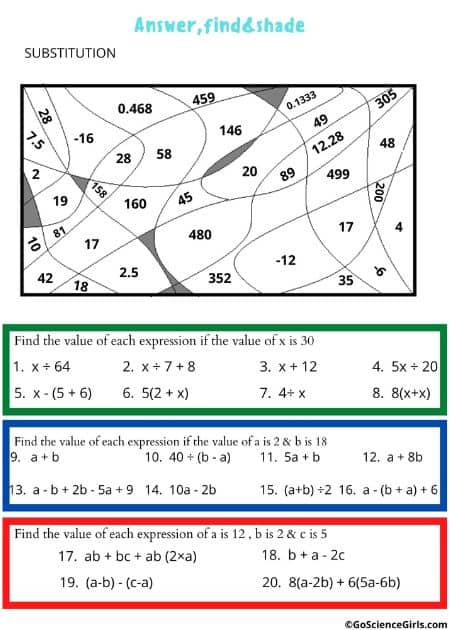

Worksheets on Substitution (Answer Find and Shade Level-2)
The worksheets at level 2 involve activities that reveal integers and decimal numbers that help in converting an equation into an algebraic equation. The alphabets are the variables in the math expressions that substitute the real values and simplify the complex expression.
Misinterpretation of Students: In an expression ab; where a = 0.3 and b = 0.3
The values of variables ‘a’ & ‘b’ are decimal numbers. So, the solution of expression is ab = 0.3 x 0.3 = 0.09. Here, students get confused to keep decimals in the solution.
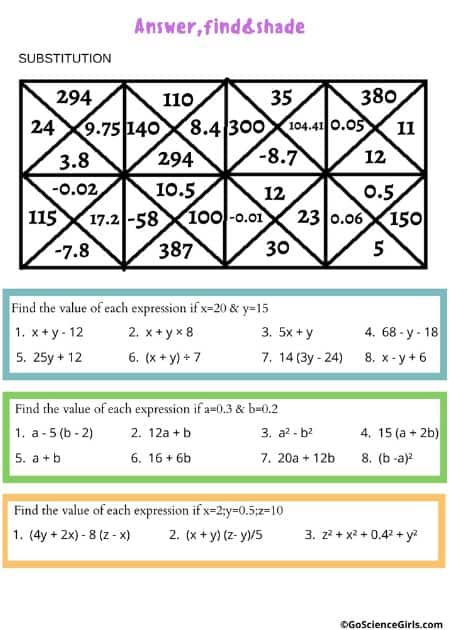

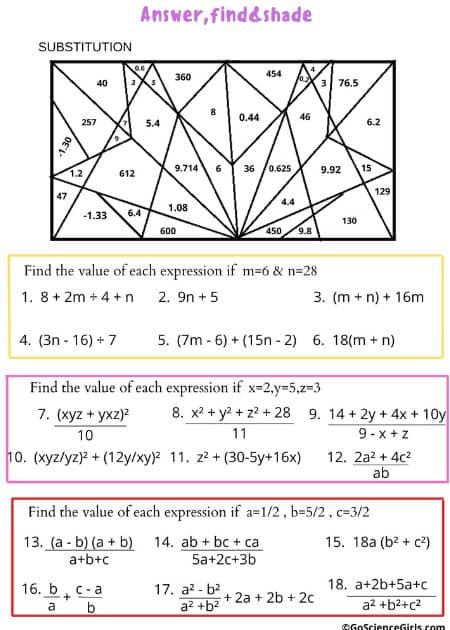

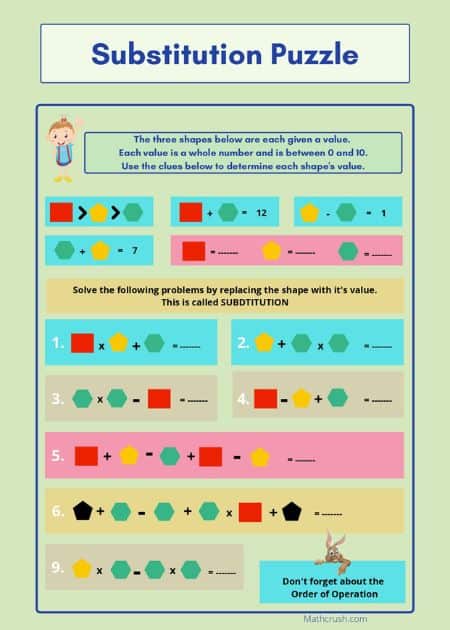
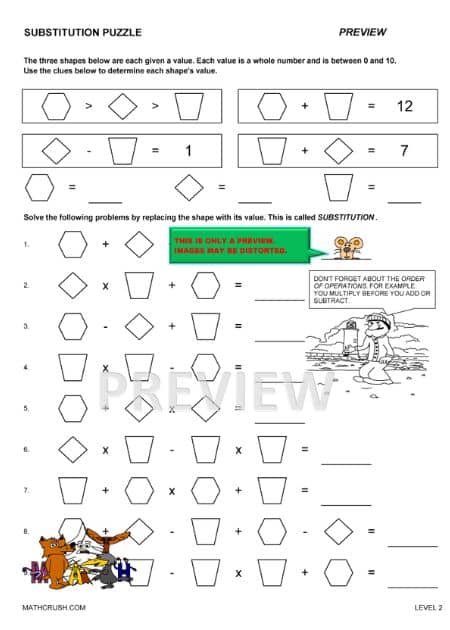
Worksheets on Substitution Puzzle (Level-2)
Students with previous knowledge of substitution numbers can match the answers to the corresponding math expression. In this way, they will find out the correct values of the patterns and convert them into expressions using derived values. Important Note: Students can easily understand the substitution numbers concept and its usage in solving math expressions by deriving variables and values.
Order of Operations – Help Packets
Order of Operations – All Levels
This six page help packet covers the Order of Operations. It starts with basic addition, subtraction,
multiplication, and division. Then introduces the left to right rule, and finishes with parenthesis and exponents.
Student misunderstanding: Most students think that multiplication should always be solved before division, and addition should always be solved before subtraction. Left to right rule.

What is Order of Operations?
In mathematics, order of operations is the set of rules that convey the order of steps to evaluate the mathematical expression to find out the answer. The PEMDAS abbreviates for the Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction. This is an easy way of remembering the order of steps to solve the mathematical calculations. Let us learn the four significant rules of order of operations that help in solving the mathematical calculation easily and in-depth.
Rule-1: The first rule of order of operations in solving the mathematical calculation present inside the parentheses or brackets. To solve the calculation present inside the parentheses, firstly consider solving inside the round brackets and then curly and box brackets.
Rule-2: The second rule is to solve the exponents if present in the same calculation. Check for the expressions that fall under exponents and crack them.
Rule-3: Thirdly, consider solving all the division and multiplication operations in the order left to right.
Rule-4: In the fourth step, solve all the addition and subtraction expressions from left to right.
That’s it! Just follow this simple and easy order of steps to solve any type of mathematical calculation, no matter the difficulty level.
Any type of mathematical calculation reveals only one answer after performing all the operations. However, the four operations that help to find out the correct answer for a mathematical expression are multiplication, division, addition, and subtraction.
BODMAS is the alternate acronym for solving mathematical expressions by following the rules of order of operations. It stands for:
B—B refers to Brackets
O—O refers to Order
D—D refers to Division
M—M refers to Multiplication
A—A refers to Addition
S—S refers to Subtraction
In this way, using either PEMDAS or BODMAS, we can solve any sort of mathematical expression and find the correct answer to it easily.
Now let us apply this set of rules used in order of operation to a few examples and understand the concept clearly and precisely.
Example-1 (Defines First Rule): 2 × (4 + 3)
Solution
In the above expression, we need to solve the calculations inside the parentheses first based on the PEMDAS and BODMAS rules.
So, (4+3) = 7;
7 × 2 = 14; this is the correct approach of solving the math expression and 14 is the correct answer for the above math expression.
8 + 3 = 11; this is the incorrect approach and you will get wrong answers at the end.
Example-2 (Defines Second Rule): 3 × (42)
Solution
42 is the term that defines the exponents, so we need to solve it first and then move to further calculations left to calculate the expression.
42 = 16, so 3 × (42) = 3 × 16 = 48; this is the correct approach of solving a math expression that involve exponents. 48 is the final and correct answer to the above question!
3 × (42) = 122 = 144; this is the incorrect approach of solving a math expression that involves exponents because 144 is the wrong answer.
Example-3 (Defines Third Rule): 3 – 8 ÷ 4
Solution
8 ÷ 4 = 2; So, 3 – 8 ÷ 4 = 3 – 2 = 1; as per the third rule of order of operation, the terms that fall under division and multiplication operators need to be calculated first.
3 – 8 = 5; So, 5 ÷ 4 = 5/4 is the wrong way of solving a math expression t6hat involve division and multiplication operators.
Example-4 (Defines Fourth Rule): 4 + 6 × 3
Solution
6 × 3 = 18; So, 4 + 6 × 3 = 4 + 18 = 22; this is the right way of calculating a math expression and 22 is the correct answer.
4 + 6 = 10; 10 × 3 = 30; this is the wrong way to calculate a math expression that involves a multiplication operator because 30 is the wrong answer.
If a mathematical expression involves all the division, multiplication, addition, and subtraction operators, then prefer to solve division and multiplication calculations first.
Now, let us solve another math expression with the help of either PEMDAS or BODMAS order of operations rule…
(2 + 22 – 4 ÷ 22) ÷ ((3 + 2)2 + 15 ÷ 3)
Step-1: Follow the first rule of PEMDAS, which is to solve the calculations present inside the parentheses.
(2 + 22 – 4 ÷ 22) ÷ ((5)2 + 15 ÷ 3)
Step-2: In the second step, follow the second rule of PEMDAS and simplify the exponents…
(2 + 22 – 4 ÷ 4) ÷ (25 + 15 ÷ 3)
Step-3: As per the third rule of PEMDAS, we need to perform division operations as the third step.
(2 + 22 – 1) ÷ (25 + 5)
Step-4: In the fourth step, we get 24 by adding 2 and 22! Later subtract 1 from 24, we get 23!
Now, the given expression after simplification is (23) ÷ (25 + 5)
Step-5: Add 25 and 5 in the fifth step and then divide the result with 23; 23 ÷ 30
The final result of the given math expression (2 + 22 – 4 ÷ 22) ÷ ((3 + 2)2 + 15 ÷ 3) is 23/30.
