In this article we have covered wide variety of Right Triangle Trigonometry Worksheets that are suitable for middle schoolers. For each section, we have given the methodology that can be used to solve the problems in the worksheet.
Feel free to download and print (for personal use) and try these intuitive trigonometry problems.
Applications of Right Triangle Trigonometry Worksheet
To solve these problems, you will have to first learn the concept of the Pythagorean Theorem and the law of tangents.
The Pythagorean Theorem –Is about the relationship between the three sides of a right-angle triangle. So, if ABC is a right-angle triangle in which the three sides are AB, BC, and AC, AB2 + BC2 =AC2. Here, AC is the hypotenuse-the longest side of the right angle triangle.
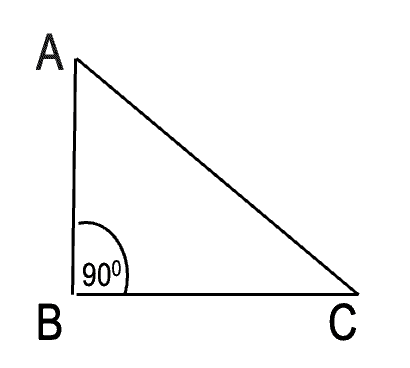
You are needed to use the above formula to determine the unknown side of the right-angled triangle when two sides are already given.
Law of tangents –It is the relationship between any two sides and the two angles opposite to these two sides of a right-angled triangle ABC. Remember, the law of tangent applies to only right-angle triangles.
Again tangent of a given angle of a right-angled triangle is the ratio of its opposite side to its adjacent side.
So, here tanC=AB/BC
Example of finding the length of a side.
Calculate the length of x and y of two right-angle triangles in the figure below that share two vertices and one common straight-line base. Here the length of one side AB is 12, D=600 and angle C=300.
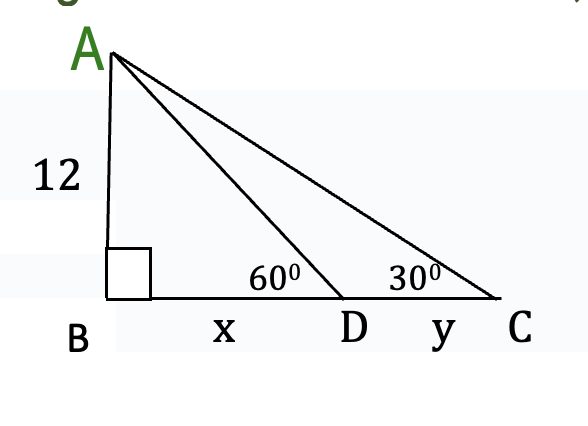
To solve the above problem, you have to do the following steps.
Step 1. For triangle ABD, you already have AB=12, B=900 and D=600
So, tan 600 =opposite side/adjacent side
=AB/BD
=12/BD
=12/x
Since it is known from the trigonometry table that tan 600 =√3, you can write
√3=12/x
So, x=12/√3
=3×4/√3
=√3x√3 x4/√3
=4√3
Step 2 For triangle ABC, you already have AB=12, B=900 and C=300
So, tan 300 =opposite side/adjacent side
=AB/BC
=12/(BD +DC)
=12/(x+y)
Since it is known from the trigonometry table that tan 300 =1/√3, you can write
1/√3=12/(4√3 +y)
So, (4√3 +y)=12x√3
y =12√3-4√3
=√3(12-4)
=8√3
Now since √3=1.732, you have
x=4×1.732
=6.928=7 (approximately )
and y=8×1.732
=13.85=14 (approximately)
Worksheet for you to try :
Basic Right Triangle Trigonometry Worksheets
To solve these problems, you have to use the law of tangents, sines, and cosines as per the given adjacent side, opposite side and the hypotenuse.
Example of finding the angle of a right angle triangle when the adjacent side and the hypotenuse are already given
Calculate the angle x of the right-angle triangle in the figure below. Here, the length of one side BC =3 and the hypotenuse AC=6.
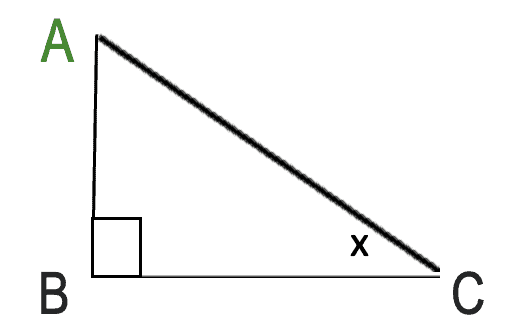
To solve the above problem, you have to do the following steps.
Since you have the length of the adjacent side of the angle C and the hypotenuse, you have to use the law of cosine.
So, cos x=adjacent side/hypotenuse
=BC/AC
=3/6
=1/2
Now, as we know cos 600 =1/2, so , x=600
Example of finding the angle of a right-angle triangle when the opposite side and the hypotenuse are already given
Calculate the angle x of the right-angle triangle in the figure below. Here the length of one side BC =14 and the hypotenuse AC=21.
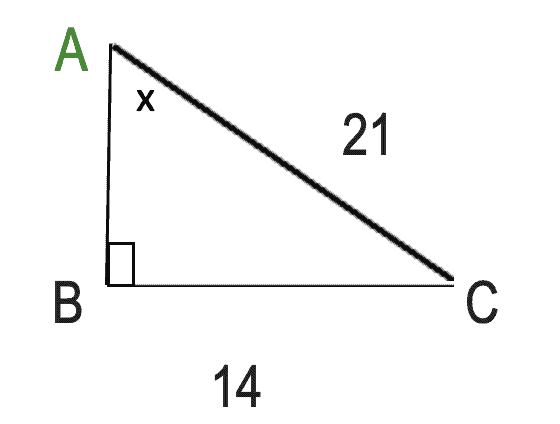
To solve the above problem, you have to do the following steps.
Since, you have the length of the opposite side of the angle A and the hypotenuse, you have to use the law of sine
So, sin x=opposite side/hypotenuse
=BC/AC
=14/21
=2/3
=0.666
Now as sin 41.80 =0.666, so, x=41.80
Worksheets to try:


Practice Worksheet – Right Triangle Trigonometry
Example of finding sin 45 degrees and cos 45 degrees of the right angle triangle in fraction form when all the three sides are given.
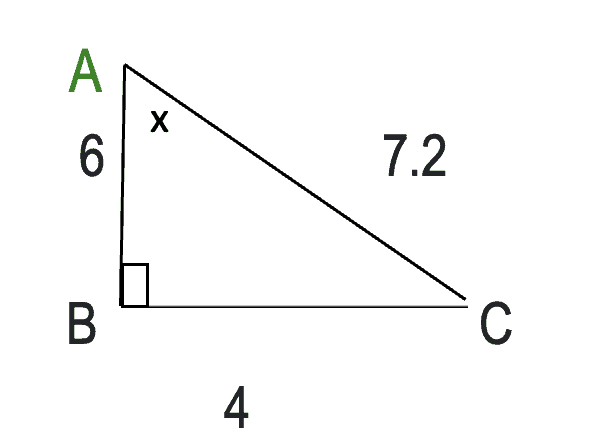
Sin 450 =opposite side/hypotenuse
= 4/7.2
=40/72
=10/18
=5/9
Cos450 =adjacent side/hypotenuse
= 6/7.2
=60/72
=10/12
=5/6

Precalculus Right Triangle Trigonometry Worksheet
Example A swimmer is 210 meter below the surface of the ocean and begins to descend at an angle of 30 degrees from the vertical. How far will be the swimmer travel before he breaks the surface of the water.
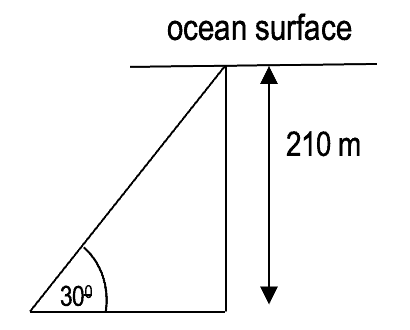
You know here Sin 300 =opposite side/hypotenuse
1/2 =210/hypotenuse [As sin30 degree=1/2]
So hyotenuse =210 ÷0.5
=420
So, the swimmer travels 420 meter before he breaks the ocean surface.

Right Triangle Trigonometry – Angle of Elevation and Depression Worksheet
To solve the problems in the worksheet, you need to first know the concept of the angle of elevation and the angle of depression.
The angle of elevation-The angle formed when an observer looks at an object above his horizontal line of sight. For example, if you stand on a plateau and look at the peak of a nearby mountain, an angle of elevation is formed.
The angle of depression-The angle formed when an observer looks down at an object below his horizontal line of sight. For example, if you stand on a plateau and look at a house in the plains, an angle of depression is formed.
Example- A bird is sitting on an iceberg 100 feet above the water. If a sea lion in water is 220 feet from the base of the iceberg, find the angle of depression.
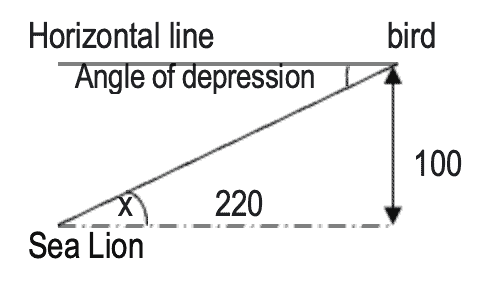
Let x is the angle of elevation that the sea lion at a distance of 220 meter from the base of the iceberg makes when he looks at the bird sitting on the iceberg at a vertical height of 100 meters.
From the above figure, it becomes apparent that tan x0 =adjacent side /opposite side
=220/100
=11/5
tan 660=2.2
Now as tan 660=2.2,you have angle of elevation x= 660
Next, we know that the sum of all three angles of a triangle equals to 1800
So, the remaining angle will be =1800 –(660 + 900) = 1800 – 1560=240
Hence, the angle of depression = 900 – 240=660
Example A 25 feet ladder leans against a house so that the base of the ladder is 7 feet from the base of the house. What will be the angle of elevation of the ladder.
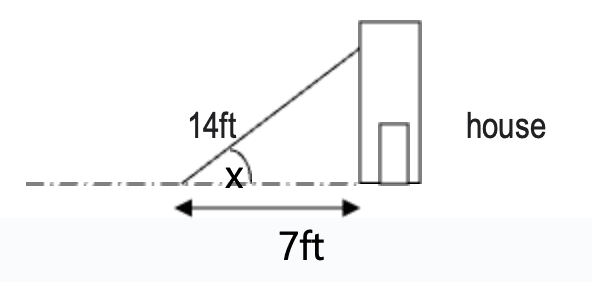
cos x=adjacent side/hypotenuse
=7/14
=1/2 [cos 600=1/2]
So, angle of elevation of the ladder= 600

Special Right Triangle Trigonometry Worksheet
Example-Half of an equilateral triangle is often called “30-60” right or “30-60-90” triangle. Explain why it is called with that name?
Since, an equilateral triangle can be split into two right angle triangles with the remaining angles being 30 degrees and 60 degrees, half of an equilateral triangle is often called “30-60” right or “30-60-90” triangle. Let us prove this with the help of the law of sine and cosine.
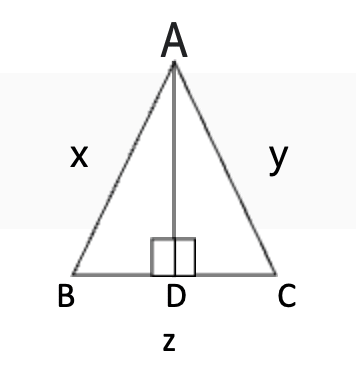
Let ABC is an equilateral triangle with sides x, y and z where x=y=z.
Now you draw a perpendicular from vertex A on the side BC, you will have two right angle triangles-ABD and ACD with angle D=900.
Next, as per the law of cosine, you know in the right-angle triangle ADC
cos C=adjacent side/hypotenuse
=DC/AC
=Half of the side z/y
=Half of the side y/y [since y=z]
=y/2 ÷ y
=1/2
Now from the trigonometry table, you know that cos 600=1/2
So, ∠C=600
Similarly, as per the law of sine, you know that in the right-angle triangle ADC
Sin A=opposite side/hypotenuse
= DC/AC
=Half of the side z/y
=Half of the side y/y [since y=z]
=y/2 ÷ y
=1/2
Now from the trigonometry table, you know that sin300=1/2
So, ∠A=300
Hence, you have in the right-angle triangle ACD, A=300, C=600, and D=900
Similarly, in the right-angle triangle ABD, A=300, B=600, and D=900

Right Triangle Trigonometry Finding Missing Sides & Angles Worksheet
Right Triangle Trigonometry Word Problems Worksheet

Trigonometry Ratios in Right Triangles Worksheet


