As part of our trigonometry worksheets collection – in this article, you will find Free unit circle trigonometry worksheets and practice problems.
What is a Unit Circle?
The unit circle is a complete circle of radius 1 and it enables you to find out the sine, cosine, and tangent of all real numbers.
Until now, you were using a calculator to find the value of sine, cos or tan of any angle in degrees, but once you have understood the concept of unit circle, you can do it yourself without any assistance from any calculating device. To understand how it works, let’s look at this circle.
Calculating Angles Using Unit Circle
Here the x-axis and the y-axis are dividing the circle of radius 1 into four quadrants. Now let the angle that the radius 1 is making with the x-axis is θ pronounced as theta and the intersection point where the radius =1 intersects with the circumference of the unit circle is (x,y).
The coordinates of the centre of the circle are (0,0), the point at which the x-axis intersects the circumference of the circle is (1,0) and the point at which the y-axis intersects the circumference of the circle is marked as (0,1).
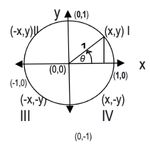
The process for determining the sine, cosine, and tangent of any angleθ is as follows:
- Step 1 –Draw a perpendicular from the point at which the radius meets the circumference i.e (x,y) to the x-axis. So, here we got a right-angle triangle!
- Step 2 -Now from the Pythagoras theorem, we know that for a right-angle triangle, the square of its long side called hypotenuse is equal to the sum of the squares of its other two sides.
So, here x2+ y2=r2 .Since here r=1, we get x2+ y2 =12 i.e x2+ y2=1
- Step 3-As per the law of sines and cosines studied earlier, we know the following things for a right-angle triangle:
- The sine of any given angle = the ratio of the length of its opposite side and the length of its hypotenuse. So, we can write sin θ=y/1=y. So, sin θ=y
- The cosine of any given angle = the ratio of the length of its adjacent side to the length of its hypotenuse. So, we can write cos θ=x/1=x. So, cos θ=x
- The tangent of the angle = the ratio of the length of its opposite side to the length of its adjacent side. So, we can write tan θ=y/x.
- Step4- Next since x=cos and y=sin, and x2+ y2=1, we can write (cos(θ))2 + (sin(θ))2 = 1
- Step 5 –We can write tan θ=sin θ/cosθ

Lessor- Known Trigonometry Functions- Secant (sec), Cosecant(csc), and Cotangent(cot)
Now that you have gained ample knowledge about sine, cosine and tangent functions, it is time to understand the concept of the three other lesser-known trigonometry ratios.
Secant (sec)-It is the reciprocal of the cosine function which implies that sec θ=1/cos θ
Cosecant(csc)- It is the reciprocal of the sine function which implies that cosec θ=1/sin θ
Cotangent(cot)- It is the reciprocal of the tangent function which implies that cot θ=1/tan θ

Trigonometry Table
To solve trigonometry problems where you need to find the value of any trigonometric ratio, you will certainly need this table. Here, the values of the standard angles like 0°, 30°, 45°, 60°, and 90°are given for sin, cos, tan, cosec, sec, and cot.
| 00 | 300 | 450 | 600 | 900 | |
| sin θ | 0 | 1/2 | √2/2 | √3/2 | 1 |
| cos θ | 1 | √3/2 | √2/2 | 1/2 | 0 |
| tan θ | 0 | 1/√3 | 1 | √3 | ∞ |
| cot θ | ∞ | √3 | 1 | 1/√3 | 0 |
| sec θ | 1 | 2/√3 | √2 | 2 | ∞ |
| cosec θ | ∞ | 2 | √2 | 2/√3 | 1 |
In the above table, the symbol ∞ represents infinity or an undefined value.
Now that you have understood the concept, let’s find out the way to find the exact value of sin, cos and tan functions if an angle θ is given as π/3 and find the coordinates that go with the angle θ= π/3.
To solve the above problem, first, we have to get familiarized with the concept of π. This is a mathematical constant, pronounced as Pie that you must have come across in maths and physics.
It is nothing but the ratio of the circumference of a circle to the diameter of the same circle. It is equal to 22/7=3.14159 (approximately) in radians and 180 in degrees.
Here it is given that angle θ= π/3
So, sin θ=sin(π/3)
=sin(1800/3)
=sin600 .
From the trigonometric table, we know that the value of sin600 = √3/2
Similiarly, cos θ= cos(π/3)=cos (1800/3)=cos600 =1/2
Now tan θ=sin θ/cosθ
= sin(π/3)/cos (π/3)
= sin(1800/3)/cos(1800/3) [Since we know π =1800 ]
= sin600/cos600
= √3/2 ÷ 1/2
= √3

Now, what are coordinates?
These are a set of values that demonstrate the exact position of a point on a two-dimensional plane.
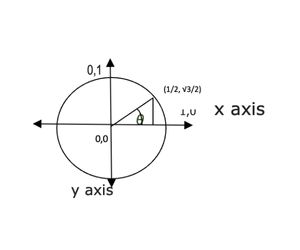
We have again made the drawing of a unit circle and marked its center, and coordinates at which the x-axis and y-axis has intersected the circle circumference.
We have also drawn a perpendicular on the x-axis from the point whose coordinates we are trying to find. From the above figure, we got that the coordinate lies in the first quadrant of the circle.
So, we can say that both the x and y coordinates will be positive.
Now we have already learned that for any given angle of a right-angle triangle, cos θ=x and sin θ=y.
But we have already deduced that here
sin θ= sin(π/3)=sin600 = √3/2 and cos θ= cos(π/3)=cos (1800/3)=cos600 =1/2
So, we need to simply put the value of x and y as the coordinates that goes with the angle θ to have our solution.
(x,y)=(1/2,√3/2)
Find the exact value of sin, cos and tan functions if an angle θ is given as -2250
Here it is given that angle θ=2250
So, sin θ=sin2250 .
Now since 2250 >1800 but a little less than 2700 , and each quadrant is of 900,
we can say that the above angle lies in the 3rd quadrant of the unit circle and sin2250 and cos2250 will be negative.
So, let’s draw the unit circle. Now here we can see that 1800 + 450 =2250 .
Now draw a perpendicular from the terminal side of the angle on the x-axis.
From the Pythagorean Theorem, we know that x2+ y2 =12 i.e x2+ y2=1
Now as here both x and y are -1, we get hypotenuse = √1+√1=√2 and by taking the reference angle of 2250 which is 450, we can say
So sin 2250 = – (length of its opposite side)/hypotenuse = -1/√2
Similiarly cos 2250 = – (length of adjacent side)/hypotenuse = -1/√2
tan 2250= sin 2250/ cos 2250 = -1/√2 ÷-1/√2 = -1/-1=1


Coterminal Angles
Two angles are called coterminal when they share the same terminal side in a standard position.
Find out the coterminal angles to angle 550
To solve this problem, let’s do the following steps
- 55°+ 360°=415°
- 360°- 55°= 305°
- 360°+360°+55°=1275°
We can calculate as many coterminal angles as we desire adding or substracting 360° multiple times.
Find out the value of tan 3π/4 by using unit circle.

To solve this problem, first of all, we have drawn a unit circle with x and y-axis.
Now tan 3π/4=tan (3×180/4) [π is equal to 180 in degrees]
=tan 1350
Since 1350 >900 but less than 1800, it must lie in the second quadrant of the unit circle.
So, we can deduce that its value must be negative.
Now, we have drawn a perpendicular from the terminal side of the angle on x-axis. Also, we have got that here the reference angle is 45 degrees.
Now tan 450 =sin450/cos450 [Since tan θ=sin θ/cosθ]
=√2/2/√2/2
=1
We know that the value of any trigonometric function of an angle is equal to the value of its reference angle.
The only change is in sign as per its position in the unit circle i.e 1st quadrant, 2nd quadrant, 3rd quadrant or the 4th quadrant.
Now since we know the value of tan1350 will be negative, tan1350= -1
Find out the reference angle of π/6.
π/6 =180/6 [Since π is equal to 180 in degrees]
=300
Now since this lies in the first quadrant of the unit circle as it is less than 900, the reference angle will be equal to the angle
So, reference angle= π/6
Let’s try to find out the value of tan π/3 if the coordinates on the unit circle are given as (1/2,√3/2) when the angle is 600.
To solve this problem, we have to do the following steps
- Since here the angle is 600 i.e less than 900, the angle is definitely in the first quadrant of the unit circle.
- We know that for any given angle of a right-angle triangle, cos θ=x and sin θ=y.
- So, we can say cos θ=x =1/2 and sin θ=y=√3/2
- Hence sin π/3=sin180/3=sin600 =√3/2 [This can be also derived from the trigonometric table]
- So, tan π/3=tan180/3
=tan600
= sin600/cos600
=√3/2÷1/2
=√3








