Algebra is one of the most basic and most used math concepts. It is the pulp of all things arithmetic and its many operations.
In simpler terms, Algebra can be defined as a combination of numbers, symbols, operations that make up an equation or expression, which one solved gives you the answer to that particular equation or expression.
In a more complex setup, a single equation is part of a set or series of equations.
There are many angles and sub-angles to what Algebra includes. Here is a complete overview starting from the basics and covering all things Algebra.
Types of Numbers
Numbers are referred to as numerical values that display a count of anything that needs to be accounted for. Examples: books, countries, population, colors, etc.
There are two representations of numbers: Numerical and In Figures. Numerical values are represented as 723, 43, 2, etc., while the In Figures are represented as Seven hundred and twenty three, forty three and two.
Numbers are classified to understand and use at appropriate places where the results yielded are most beneficial. The major divisions are given below:
Real Numbers
All numbers that are positive, negative, zero, and can be represented on a line are called Real Numbers. Example: -2, 0, +4, etc.
Real Numbers include Rational and Irrational Numbers.
Rational Numbers
It is simply the ratio of an integer to a non-integer, or all numbers that can be expressed as fractions are called Rational Numbers. Examples: 2/3, -18/4, etc. Also called Non-Irrational Numbers.
Irrational Numbers
As the name suggests, it is the opposite of what a Rational Number shows. Meaning, numbers that cannot be expressed as fractions are called Irrational Numbers.
Examples: 9, 4, 13, etc. Also called Non-Rational Numbers.
Integers
The numbers that are the exact opposite of Whole Numbers are numbers beginning from 0 to infinity. They include both positive and negative whole numbers.
The negative integers are represented with a minus sign as a prefix to the number. Example: -9.
While the positive integers are represented with a positive sign as a prefix to the number. Example: +12. But, most of the time, the positive sign is not written, which automatically implies that the number is a positive value and not a negative value.
The below worksheet covers real numbers. Students learn about rational and irrational numbers, and answer problems related to each set.
Key concept: Students know the difference between rational and irrational numbers, and understand patterns and structure.


Types of Numeral Systems
There is no one particular method of Numeral System representation. If there were, it would be difficult to express certain numbers in one format only, hence the need for different Numeral Systems.
Decimals
Decimals are represented by a simple ‘.’, just like a full stop/period. However, where it is placed makes a huge difference.
For instance, you bought a watch for $13.44. If you accidentally misplace the dot once left or once right, the cost would change to $1.344, or $134.4, which creates a difference of one entire digit and a hundred dollar difference.
Therefore, Decimal plays a vital role in displaying cost, weight, length, etc.
Numbers after (from right) the Decimal point are of lesser value than those before the point. Taking the example of the above watch, since 100 cents make up 1 dollar, there are still 56 cents before the dollar is complete, and the 13 becomes 14.
Fractions
In a way, Fractions can be called expanded forms of Decimals. Why? Because you can write 0.25 as ¼ in Fractions.
Fractions show a part of the whole. They can be anything to everything: a slice of the whole pizza or the number of books you readout of the total available in your library.
Example: If half of the Pizza you ordered is eaten out of the whole you ordered, how do you represent it in fractional form?
Solution: Whole is always ‘1’, and a part of it will always be less than 1. However, note that if there are more than 1 wholes, the count increases, and then the fractional part is written.
For the Pizza eaten out of the whole, representation is – ½. Since you have divided the whole Pizza into two equal parts, 1 of which you ate, it is shown as above.
The clarification is because you may doubt how 1 Pizza became 2, as the number in the denominator is 2 instead of 1. Fraction always considers total parts and then gives the value of what is asked.
Exponents
Suppose you have an expression where you need to multiply one term several times. Instead of writing the term the respective number of times, you can simply write the term once, and then on the upper right corner of the term or superscript in slightly smaller font, you can write the repeating number.
Example : 3 x 3 x 3 x 3 x 3 x 3
Solution: 36, here the term or number 3 has been multiplied 6 times. So, the superscript number is 6. The answer is 729
3 is said to be the ‘base’ number, while 6 is said to be the ‘Exponent.’
Verbally, this is spelled as – ‘ this is third to the sixth power.’
There are short verbals for a term repeated only twice or thrice. They are ‘squared’ and ‘cubed,’ respectively.
Therefore, if we modify the above example expression to 32 and 33, 3 squared is 9, and cubed is 27.
Types of Representations
There are various patterns of how you can represent a certain amount of something. Let us look at some of the more commonly used representations with examples to understand the representations better.
A tabular format or a table is a combination of a certain number of rows and columns. Each row and column represents a different heading that is interrelated.
Tables
Data is gathered in this table, with proper segregation for better comprehension of what it is displaying. However, it can be challenging to understand what number is accountable for what category when you have too much information.
Therefore, Frequency Tables were born.
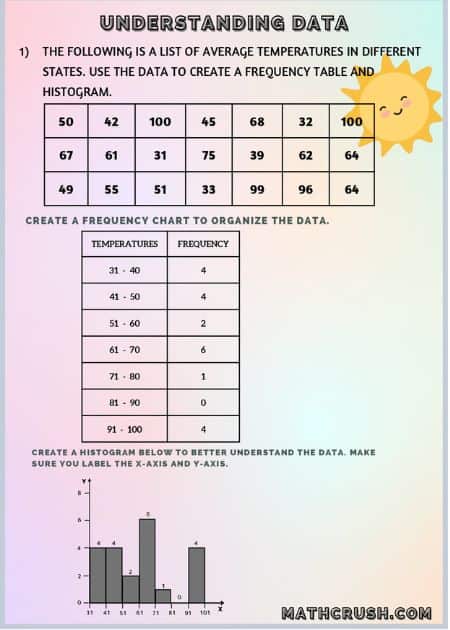
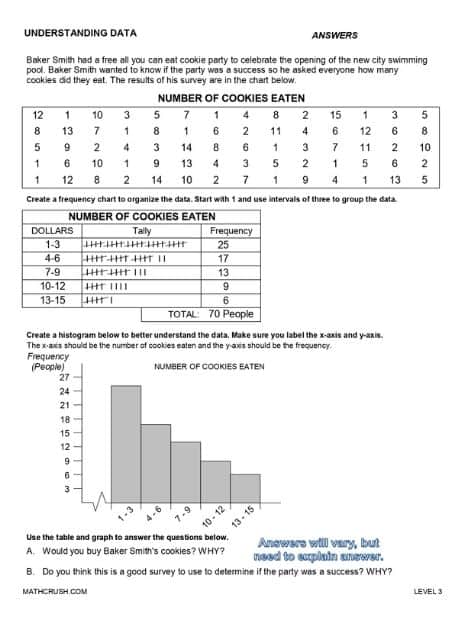
The below worksheet covers tables and graphs


Frequency Tables
The most basic Frequency Table has 3 columns. At the top, a horizontal row heading of what the table is about is mentioned.
Next, the table is divided into 3 vertical columns (or more, depends on data type), each with a different heading. The horizontal rows are also decided upon how the data is being divided. There is no limit to both rows or columns.
Example: Runs made by each player of a Cricket Team are given as – 21, 33, 1, 78, 2, 34, 2, 2, 45, 66, 0. How do you calculate the Frequency of how many players earned runs in a certain range?
Method: First and foremost, divide the table into three vertical columns, with the three headings as – Runs, Tally, and Frequency. Also, Tally is nothing but a stick number representation of each count.
In the first column, write the ranges as 0-10, 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, and 70-80.
You can even take broader ranges such as 0-40 and 40-80, but that will be difficult to understand since we have more values with smaller ranges. The same is the case with taking smaller ranges such as 0-5, 5-10, etc.
In the next column of Tally, let us draw sticks of the first range. Players that scored runs between 0-10 are 5. So, draw five lines.
Remember, always draw 4 separate small vertical lines and then a diagonal from top left to bottom right finishing 5. If the value is less than 5, then no striking is required.
In the final column of Frequency, you will simply have to write the number, same as the tally, but in a numerical value.
Graphs
Graphs are of many types that showcase different days in different manners. There are bar graphs that show comparable, and then there are pie charts that display what is occupying more and what is occupying less.
Histograms
Distinct to Algebra, Histograms is a diagrammatic representation of the data given. Comparison is one of its principal aims.
If we retake the above example, the Runs range value will fall on the x-axis and the number of players, i.e., the frequency on the y-axis. Drawing all the individual bars will give you a comparative picture of how many runs in a range were scored by how many players.
There are no gaps between each bar. This makes a Histogram differ from a Bar Graph.
Expressions
Expressions are simply a combination of numbers, symbols, and operations. Out of the three mentioned constituents, a combination of two is what divides the general Expressions.
Numerical Expressions
Symbols are used to write an operational expression. Words are not used.
Example: 7 + 3 = 10


Verbal Expressions
Exactly as the name suggests, verbal refers to words only explanation of any mathematical concept. Numbers are also involved, but the operation being carried out is spelled out.
Example: A numerical expression is written as 7 + 3 = 10, while a verbal expression is represented as 7 plus 3 equals 10.
Also, there are many aliases to each operation. For instance, instead of ‘plus’ as in the above example, you will see or can use the sum of, increased by, added to, more than, etc.

Constants
As in the English language, we use Constant to define something that remains the same, no change whatsoever; it is used for the same purpose in Algebra. It depicts fixed information, as in amount or quantity, about the object in question.
For example, in the equation – 2 + 3 = 4b, the constants are 2,3, and 4.
Variables
Similar to how numerical and variable expressions are opposite to each other, Variables are opposite of Constants. The former is fixed, as mentioned earlier, whereas the latter is changing, always, constantly.
The use of alphabets A-Z denotes variables. Out of the 26, the most used are a,b,x,y,z, etc.
Let’s retake the above example to avoid any confusion and a better understanding. So according to the equation – 2 + 3 = 4b, ‘b’ is the variable.
Variable Puzzles are another way of representing Expressions. Each variable is assigned a specific value, and then the expression must be solved using the clues.
If the expression is C – 2B + A, and the values for the Variables A, B, and C are given as 1, 2, and 3, what is the final value of the entire expression?
C – 2B + A
1 – 2×2 + 1
1 – 4 + 1
1 – 5
-4
Substitutions
This placing of values in place of their respective representations is called ‘Substitution.’ In the above equation, 2B means 2 multiplied with the designated value of 2 and not the number 22 as may be mistaken due to the absence of the multiplication symbol.
There are times, where the variable doesn’t need to be fixed to be Alphabets only. They can be shapes, objects, animals, anything that constituents for the actual value to be used in the equation.
Substitution is a concept you will be using in many physics and chemistry in the form of formulae. So you must understand where, when, how, why and what to substitute in each expression given to solve the problem with accuracy.
A level one example: Calculate the distance traveled by a Car, running at a speed of 90 kmph for 3 hours.
Distance = Speed x Time
d = s x t
d = 90 x 3
d = 270 km
Similarly, there is a whole lot of formulas that require substitution to find out the unknowns.
Why are Expressions important in maths?
An Expression, whether Verbal or Numerical, gives a complete idea of how the equation works. Simply having numbers or letters put together won’t help solve the problem anyway. Hence the need for Expressions.
Order of Operations
This is one of the big problems you might face. In what Order do I go about solving the equation if it has multiple Operations in it? Where do I begin? Left to right or the opposite?
Well, here is a simple and easy-to-remember acronym – BODMAS, that expands to ‘Bracket of (or Parenthesis) Division, Multiplication, Addition, and Subtraction. All you need to do is follow the order given in the expansion.
Note: Remember, if the entire equation is within brackets, then follow the BODMAS rule. If the equation has operations before the brackets, then also follow the same, except for the BO part, obviously.
An example will help you grasp the concept quickly. So, here is one –
22 – 3 + 7 ( 4 x 3 ÷ 2 ).






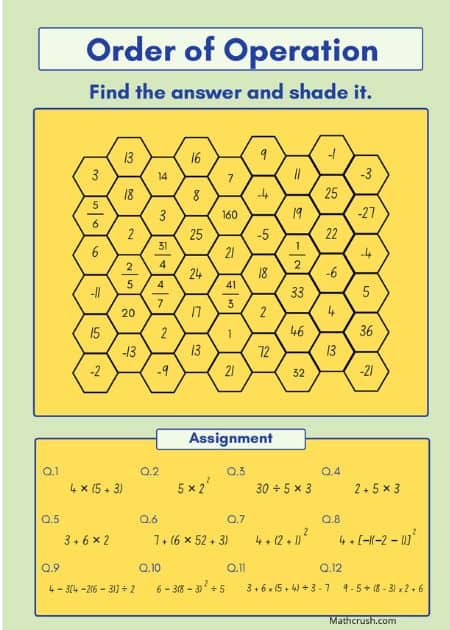

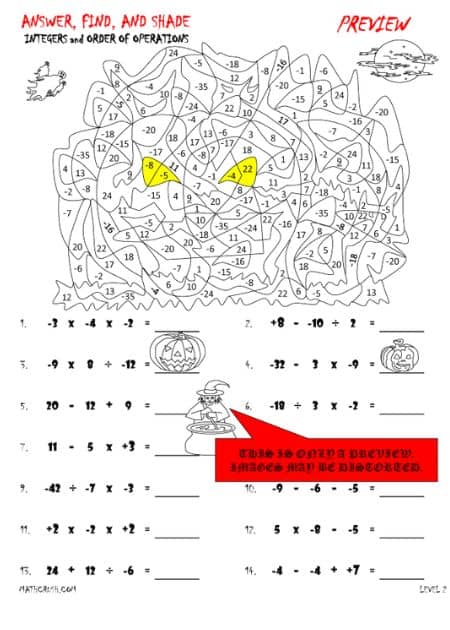
BODMAS Rule
Start with the bracket part. First, solve the equation 4 x 3 ÷ 2.
Like I explained earlier, follow the acronym. So, according to that, first up is Division.
3 divided by 2 is 1.5
The equation is now – 4 x 1.5. Multiplying this will give you 6.
The further solved equation is – 22 – 3 + 7 (6). Any number within brackets is always in multiplication.
Therefore, now the equations is – 22 – 3 + 7 x 6.
Following the DMAS rule, we move on with the solution-finding.
Multiply 7 with 6. You get 42.
22 – 3 + 42
Add 3 and 42. You get 45.
22 – 45
Finally, Subtract 45 from 22.
The final answer is – 23, a negative integer.
Hence, from the above example, you understand how the Order of Operations works and the order to be followed for Division, Multiplication, Addition, and Subtraction.
Also, from the previously learned concepts, you came across a Decimal and a Negative Integer. And, this is how various ideas converge in one Algebraic Equation.
No need to worry if you get your answers in not Whole Numbers. Fractions, Decimals, Positive or Negative Integers are also correct answers. In fact, you may also get equations that may have such numbers in the beginning equation itself.
The method to solve them is the same as regular or whole numbers. No unique approach is to be used in their case.
Before we move on with the next set of concepts, you may have one question: What if we have brackets within brackets? How do we solve that?
To answer that, you should solve the innermost bracket first and then move outwards, irrespective of the number of brackets—Centre to Periphery.
This way, you won’t have to redo the entire problem since you will have the correct answer at the first attempt itself!
Simplifying Expressions using Operations Properties
Simplifying Expressions does not need Variables or Constants to be aligned to solve, unlike Variables and Constants cannot be solved altogether.
You can solve them in their original places, and Operation Properties came into existence to help you with that.
Algebraic Operations, aside from using a proper order, require a set of Properties, like rules and regulations, that you must abide by to arrive at the correct answer.
If you do not follow them carefully or deviate even the slightest, the probability of you arriving at the wrong answer increases significantly.
Therefore, there are specific Properties set in place to avoid any straying from the original plan.
There are a major set of 4 Properties that you must follow, without any exceptions, to solve any Algebraic Equation.
Distributive Property
Distribution is the key to this property. It is a multi-step property.
It aids in easier and quicker solving, especially in bigger, longer equations with three or four-digit numbers.
Example 1 : 7 (5b – 2)
Solution :
Distributive property works by multiplying the number outside the bracket, first with the first term or the term left of the operational symbol and second with the second term or the term right of the operational symbol.
To simplify this, let us solve this using the numbers given in the example equation.
Multiply 7 with 5b, resulting in 35b. Then, multiply the same 7 with 5, resulting in 14.
The simplified equation will be 35b – 14; final answer.
Example 2 : 3 x 42
Solution :
This second example focuses on the other version of how you can use the Distributive Property to solve larger numbers.
Separate the second term of the equation into its simpler constituents of two. In this case, you can go for 40 + 2 for 2.
Now, the equation will be 3 ( 40 + 2 ). From here on, you can use the same method of solving as the first example.
Multiply 3 with 40 and then with 2. The equation will come to around 120 + 6, on the addition of which you get 126 as the final answer to the comparatively harder equation than the first.
Some worksheets below that deals with the distributive property.
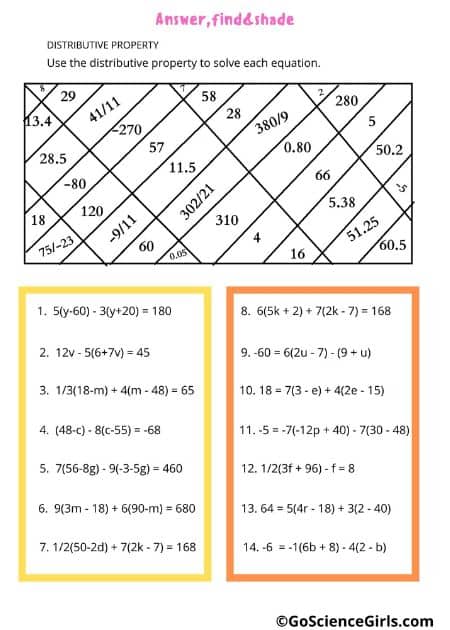
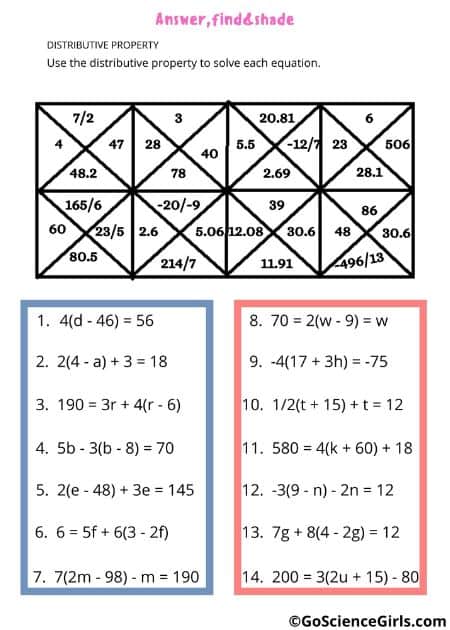
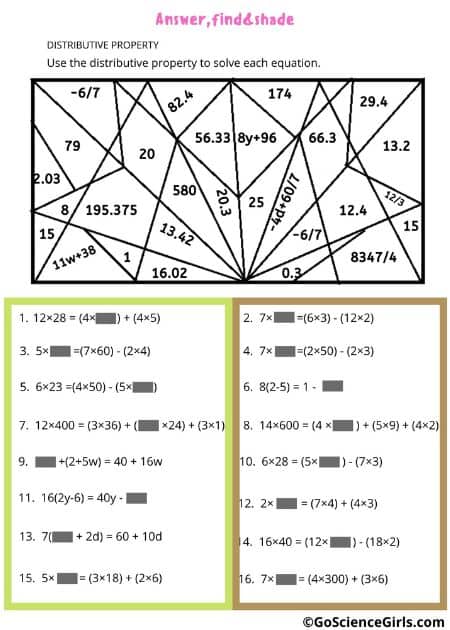
The Distributive Property of Multiplication
The below video covers The Distributive Property of Multiplication. There are three different levels of worksheets to go with the video.
Level 1 covers only addition, level 2 covers addition and subtraction, and level 3 covers algebraic expressions. Each worksheet includes basic practice and an Answer, Find, and Shade
Activity, which can be used separately.
Video Link : The Distributive Property of Multiplication



Multiplying Larger Numbers Using the Distributive Property – Level1
The below worksheet uses the Distributive Property to multiply larger numbers.

The Distributive Property of Multiplication Word Problems – Level 2
The below worksheet uses the distributive property of multiplication to solve word problems.

Answer, Find, and Shade Distributive Property



Binomials
Multiplying Binomials is a subpart of the Distributive Property.
Binomials refer to two expressions that already have an operation to be performed with themselves.
Example : ( 4 + 5 ) ( 2b – 6 )
Solution: To solve a multiplying binomial, you will have to follow the ‘FOIL’ Rule, which expands to – First Outer Inner Last.
By following the FOIL rule, you will have to go forward multiplying exactly like the following steps:
The first term of the first binomial with the first term of the second binomial; 4 x 2b = 8b
The first term of the first binomial with the second term of the second binomial; 4 x – 6 = – 24
The second term of the first binomial with the first term of the second binomial; 5 x 2b = 10b
The second term of the first binomial with the second term of the second binomial; 5 x -6 = -30
The resulting equation: 8b – 24 + 10b – 30
Solving further, 18b – 54.
Commutative Property
With respect to Commutative Property, it is the one out of the four that deals with rearrangement of terms but is strict with the symbols they carry.
Meaning, if you wish to change how the terms are arranged in an equation or expression, you can do so. However, keep in mind that you should avoid forgetting or misplacing the sign the term was initially commutated with.
For instance, in the equation – 4x – 2b + 32, you can change the term placements in the following five patterns,
4x + 32 – 2b
– 2b + 4x + 32
– 2b + 32 + 4x
32 + 4x – 2b
32 – 2b + 4x
Observe how with the changing positions of each term, the sign is also changed with them. This does not change the core principle of what the expression is about.
If you do not adhere to the changing signs with the numbers, then the entire expression changes, thus, completely changing the expression in its entirety.
Therefore, Commutative Property, though it may seem too simple, is one of the four crucial pillars like the others.
Commutative Property – Level 1
These one page worksheets introduce the Commutative Property of Addition. Students see that the order does not matter and by moving numbers around it can help them solve more complex problems. There are two different versions.


Commutative Property – Level 2
One page worksheets continuing the Commutative Property of Addition. Students use the idea that
order does not matter to solve more complex problems. There are two different versions.
Key concept: Get students thinking of ways to save time and effort.


Commutative Property – Level 3
These one page worksheets finish the Commutative Property of Addition. Students should see
that the order does not matter, and can save time and effort by moving numbers around. There are two different versions.


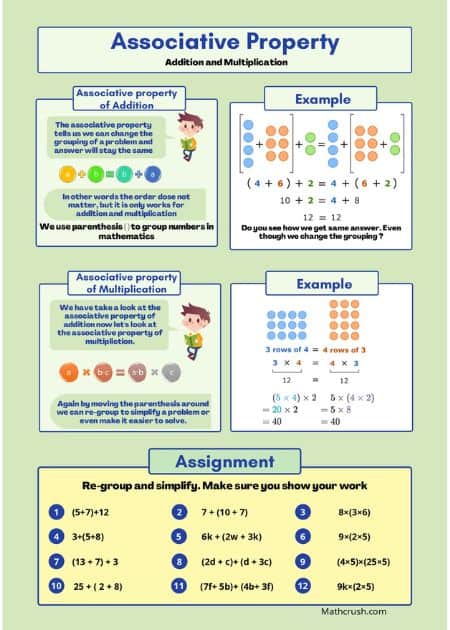
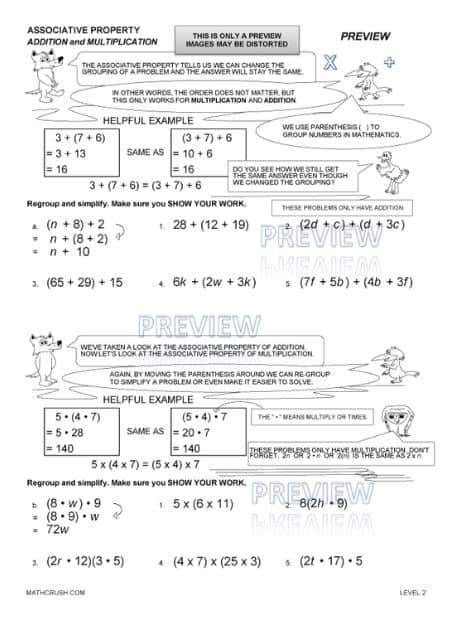
Associative Property
In an Equation, mostly, brackets mean Multiplication. But, if there is a symbol before the opening bracket or after the closing bracket other than Multiplication, then the sign should be considered for the operation to be carried out.
Now, if the sign showing an operation is the same within and outside the bracket, and the bracket is displaced, it is irrespective of the answer.
Example : 4 + (34 + 6) = (4 + 34) + 6
Solution: Now, How do you prove that both the expressions give the same answer. Here’s how –
First, let us solve the left-hand side part of the equals to sign:
4 + (40)
4 + 40
44.
Then, let us solve the right-hand side part of the equals to sign:
(38) + 6
38 + 6
44.
Hence, the aim of Associative Property is fulfilled. You can try other examples taking Subtraction, Multiplication, and Division as the operation type, and you will find that the result you reach will be the same.
The below worksheet deals with the associative property.
Associative Property of Addition
Level 1
This one page worksheet introduces the associative property. It explains how we can change groups (move parentheses) in a problem to make it easier to solve.
Key concept: Students need to understand that the order does not matter when adding. Numbers and groups can be moved to help us simplify a problem or make it easier to solve.

Associative Property of Multiplication
Level 1
This one page worksheet introduces the associative property. It shows that we can change groups (move parentheses) to make problems easier to solve.
Key concept: Order does not matter when multiplying. Numbers and groups can be moved to help simplify a problem or make it easier to solve.

Simplifying Expressions
This worksheet covers simplifying expressions. Students need to combine like terms using basic arithmetic and the associative,
commutative, and distributive properties.





This worksheet continues simplifying expressions. Students need to combine like terms using basic arithmetic and the associative,commutative, and distributive properties. It includes using the distributive property with fractions.
Note: If terms differ in at least one variable, then they are unlike terms and cannot be combined.

This worksheet finishes simplifying expressions. It includes using the distributive property with fractions and multiple variable and square terms. Students need to combine like terms using basic arithmetic and the associative, commutative, and distributive properties.

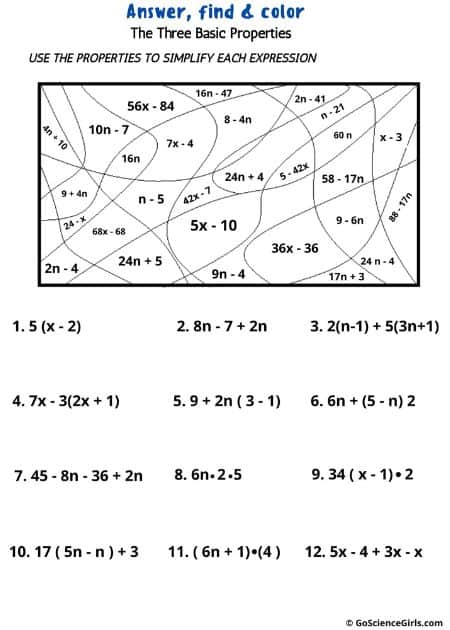
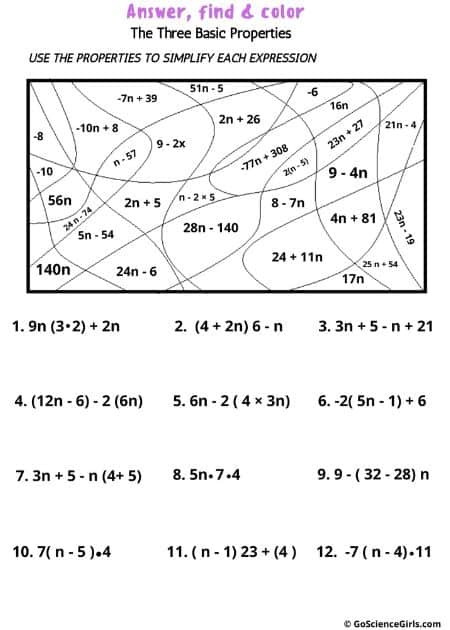
The below worksheets have students use the distributive, associative, and commutative properties to simplify expressions.
The drawing is the same but the shading and questions are different for each worksheet.
Answer, Find, and Shade Three Basic Properties
The below worksheets have students use the distributive, associative, and commutative properties to simplify expressions. The drawing is the same but the shading and questions are different for each worksheet.
Answer, Find, and Shade Arithmetic with Rational Numbers
Below art worksheet reviews arithmetic with rational numbers, positive and negative integers, fractions, and decimals.
Identity Property
The most uncomplicated property of all the four states that any expression, equation, term, constant, or variable multiplied with ‘1’, will be equal to the same expression, equation, term, constant, or variable as the original.
Example : (3b + 12a) – (22b + 33a) x 1 = (3b + 12a) – (22b + 33a)
| Point to Remember: When multiplying signs, you will need to remember the following four principles not to make any mistakes or interchange them in the calculation. – x – = ++ x + = +- x + = – + x – = – To make it even easier for you, remove the last expression, as the third and fourth expressions are the same, and give you the same result. This is because, in Multiplication, the interchanging of terms does not affect the outcome. |
Exponents
The below worksheets covers basic exponents. It includes a short help section to help students better understand exponents.
Note: Students need to know that a number to the second power is the same as calling it squared and a number to the third power is the same as calling it cubed.
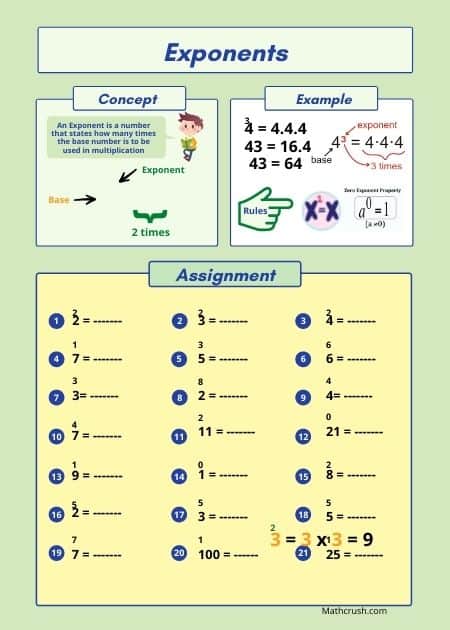

Squares and Square Roots
Square Roots are the opposite representation of Exponents and restricted only to being multiplied twice and not more than that. Rather than displaying the number ‘2’ as a superscript, to the term squared, a √ is added to it.
A visual representation of the square root is –
Exponential Format:
22 = 4
Square Root Format:
2 = √4
You cannot write both the Exponential and Square Root Formats together as ‘22 = √4’. This is not allowed. You can write either of them, but not both.
It is not mandatory that all the numbers have their perfect squares. Sometimes, the answers are in Decimals, or Fractions, or even the questions and are stated as Non – Perfect Squares.
The examples below will help you understand better –
Perfect Squares
Example : 11 x 11 = √121
Here, you have no residual number, whether you dissociate 121 to 11 x 11 or multiple the two 11s. No remainder.
Non – Perfect Squares
Example: √31
Here, when you dissociate 31, you do not get equal two numbers like 25 by multiplying 5 with 5, or 36 by multiplying 6 with 6, hence the term non-perfect square.
Now the question of where to place it? 5 or 6? The closer the number, the more accurate is the square value. Since 31 is closer to the square of 6 than 5, you can approximately equal the square root of 31 to 6.
The Worksheets below shows the detailed examples





Answer, Find, and Shade Squares and Square Roots
The below art worksheet reviews squares and square roots. The square roots are perfect squares so students will not have to estimate and no irrational numbers will be left over. Watch out for the decimals.

Estimating Square Roots
The below worksheet introduces estimating squaring roots of irrational numbers (not perfect squares). Students estimate the square root to the nearest whole number.


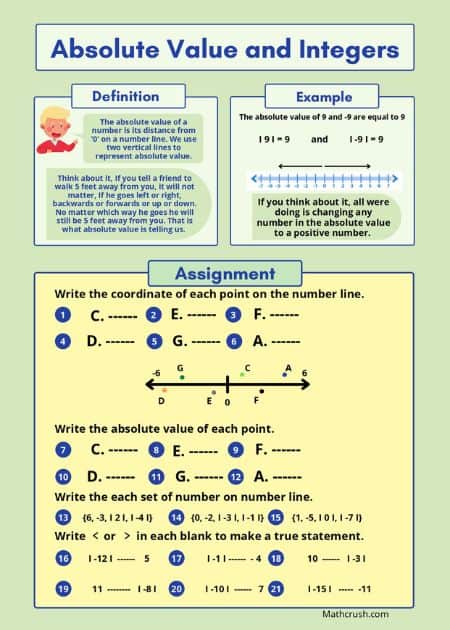
Absolute Values and Number Lines
Number Line is a horizontal line representing different numerical values beginning from the center as 0 and then continues in both directions at regular intervals, placing numbers in increasing order.
As we learned earlier, numbers, or rather integers, are both positive and negative. If you draw a number line, extending on the right will be the positive numbers, and then on the left in extension will be the negative numbers.
Coming to the actual concept of Absolute Value, it refers to the value or count of anything measured beginning from zero to the current position of that thing.
Again, an example is necessary to understand. Let’s suppose you let your pet out for a walk from your house to the nearby park.
Irrespective of whether your pet goes left, right, forward, backward, or even diagonal, if it takes 20 steps to reach the park, it will be counted as 20 steps only.
If your pet goes left or down, it does not mean that it is -20 steps. The negative sign is immaterial here.
The below worksheet introduces absolute value and reviews number lines. It explains what is the absolute value of a number and includes problems with number lines, greater than and less than, and solving simple expressions.

Unit Rate
Rate or Unit Rate is the measurement of a trend or repetition in data. Hours, minutes, seconds, days, weeks, years, classes, etc., anything from which a smaller quantity can be extracted and represented of the total.
Assuming you drink 1 glass of water every 3 hours, the rate of you drinking water in a day will be 8 glasses in 24 hours.
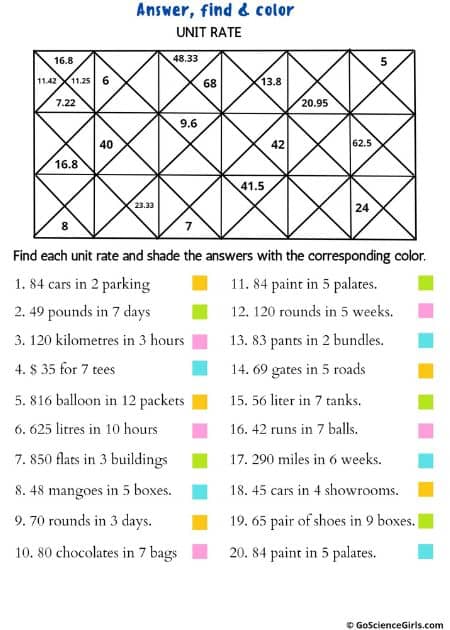
The below worksheet is a new idea we call Stained Glass. The picture is symmetrical and students choose
their own colors to create a unique art project. The worksheet covers unit rate and students answer the problems, find the numbers in the picture, and color the shapes based
on the colors they chose.

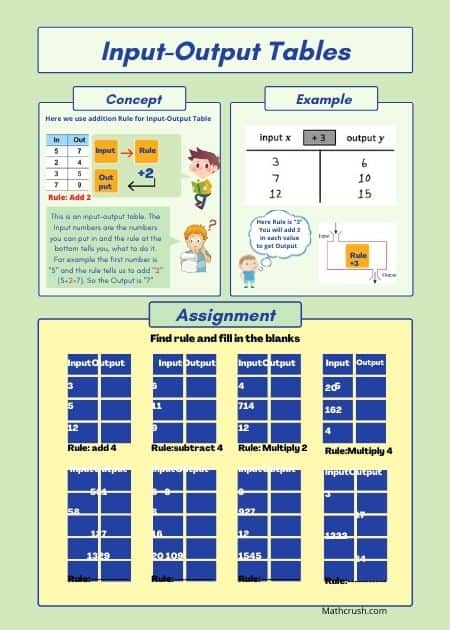
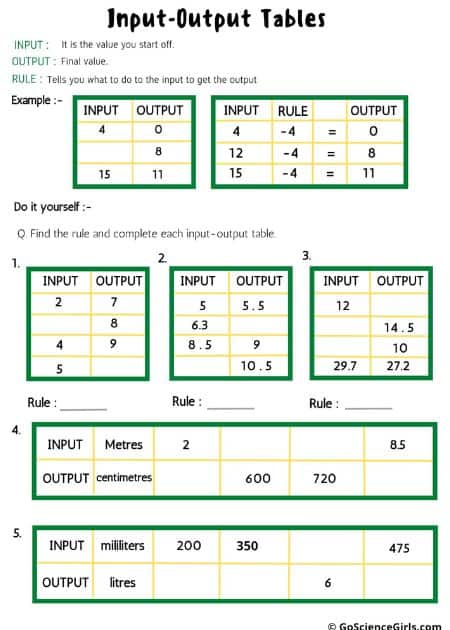
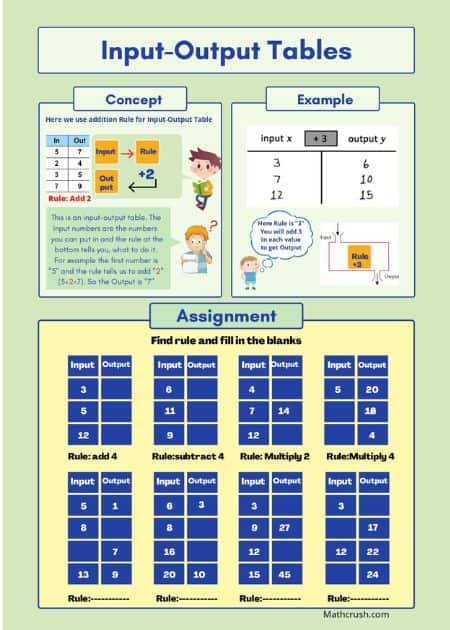
Input-Output Tables
A rule is fixed to each Table. You must follow the rule to carry out the operation of Input-Output.
Input meaning insertion of data, and Output meaning exertion of data. In between the two primary functions, you will have to use the rule of that table.
For example, the rule for a set of values is ‘Addition of 23 to each’. Out of the set, the first Input value 65. Find the Output.
So, add 23 to 65. 88 is the answer and the first Output value of the table.
And this is how Input-Output Tables work. Data is given. Follow the Rule prescribed to each. You will have a correctly filled table before you in no time.
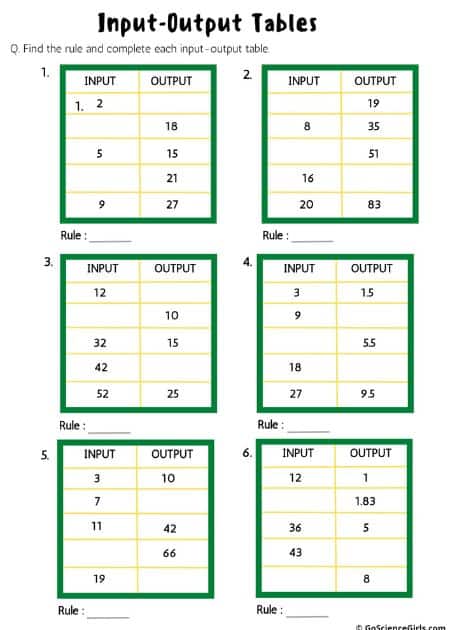
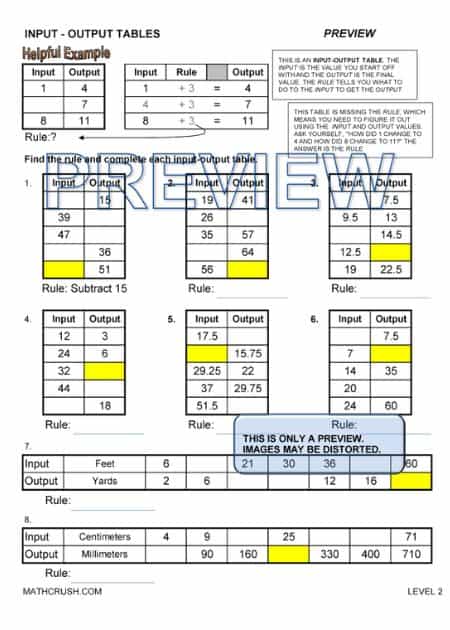
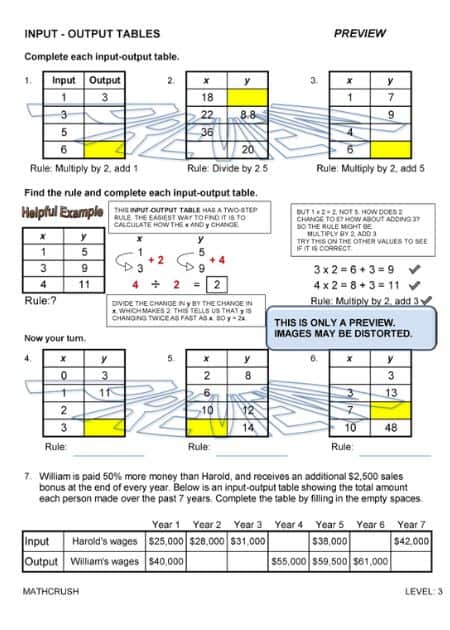
The below worksheets cover input-output tables. Students need to find the rules and complete the tables. Input-output tables help students recognize patterns and build a relationship between lines and equations. There is a different worksheet for each level.

Variable Puzzles
These one page worksheets use puzzles to help kids practice their algebra skills. Students are given five variables (letters) and have to find what numbers they represent. They are given equations as clues and a grid to help solve the unknown variables. This can also be used to practice the
process of elimination for test taking skills.



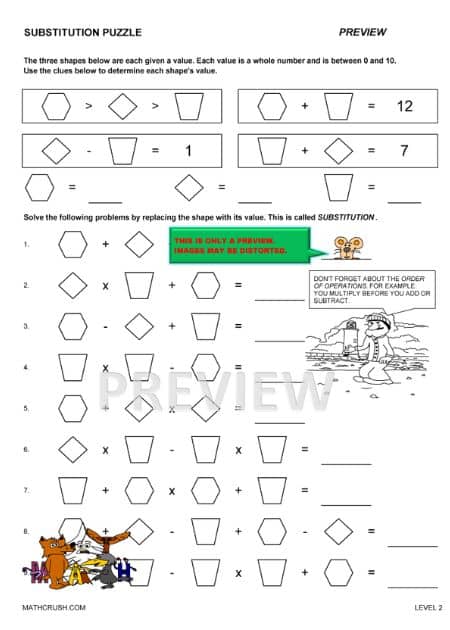
Substitution – Level 1
The below worksheets introduces substitution. It has worksheet for addition and subtraction, and for multiplication and division.










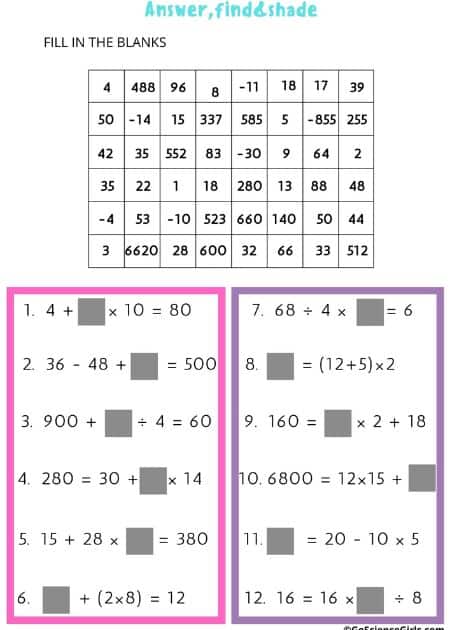
Answer, Find, and Color – Level 1 Fill in the Blank
The below art worksheet reviews basic order of operations by having students fill in the blanks to
complete various equations.

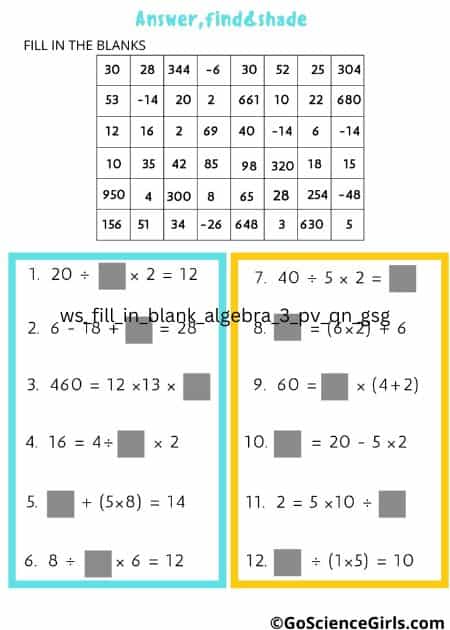

The below art worksheets use fill in the blank questions to review order of operations and solving equations. The drawing is the same but the questions are different for each worksheet.



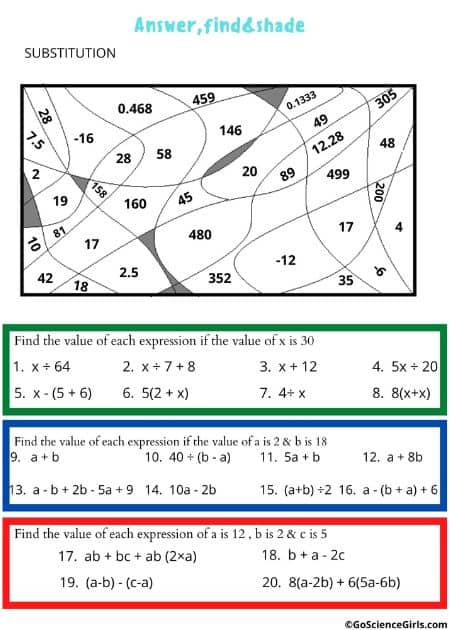
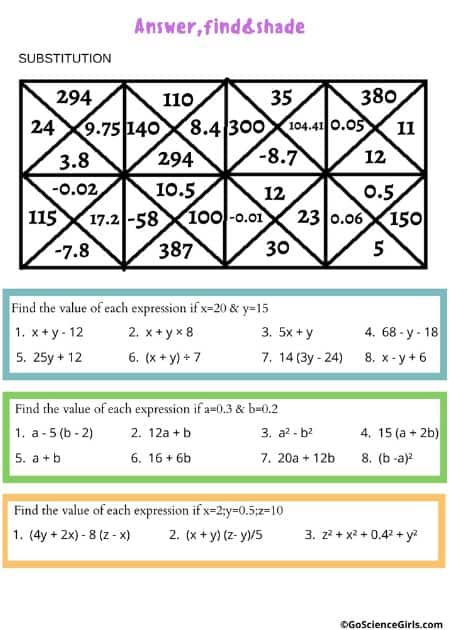
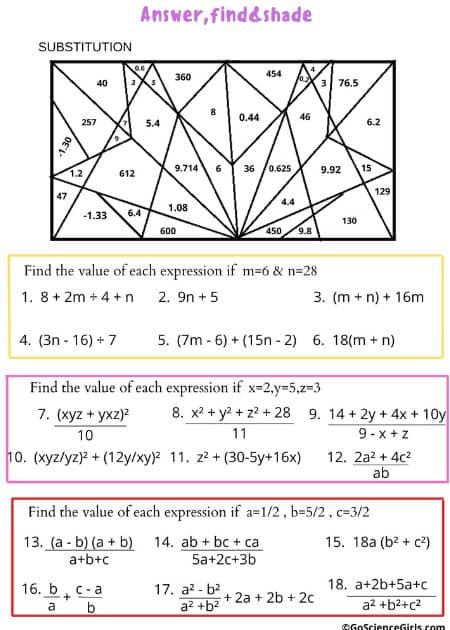
Answer, Find, and Shade – Substitution
The below worksheet reviews substitution, order of operations, and basic algebra. Students substitute the values into the expressions and solve.



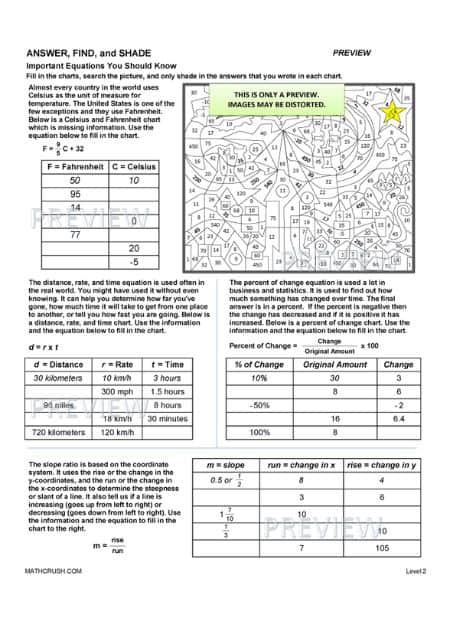
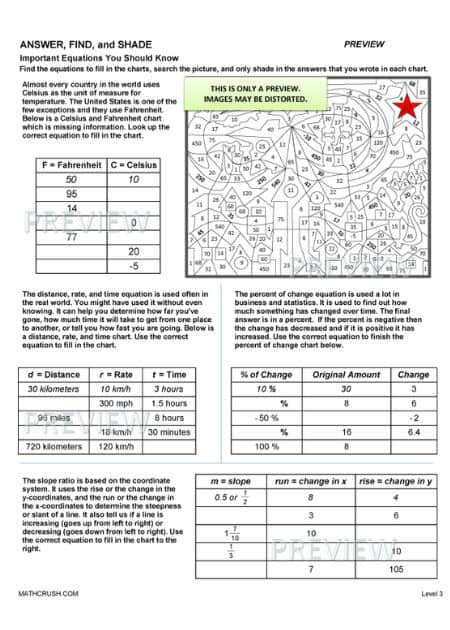
Answer, Find, and Shade Important Equations
The below worksheets review solving equations, substitution, charts, and learning real world equations. Students are given a chart and must fill in the empty spaces.



Solving One-Step Equations Addition / Subtraction
The below worksheet covers basic one step equations using the opposite operation method.



Solving One-Step Equations Multiplication / Division
This two page worksheet covers basic one step equations using the opposite operation method.



The Basics Art – Level 1
This below HALLOWEEN worksheet is a basic algebra practice page. Students use addition,
subtraction, multiplication, and division to solve one step equations.


One-Step Equations
The below worksheets covers solving one-step equations. It includes addition, subtraction, multiplication, and division. Students answer the problems and then shade in the
corresponding shapes to create a picture.
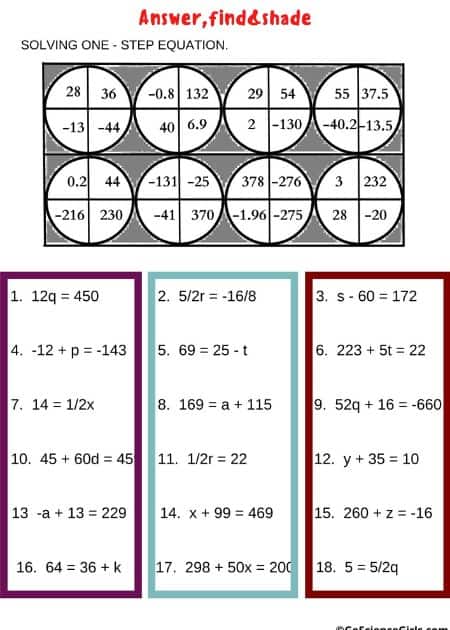
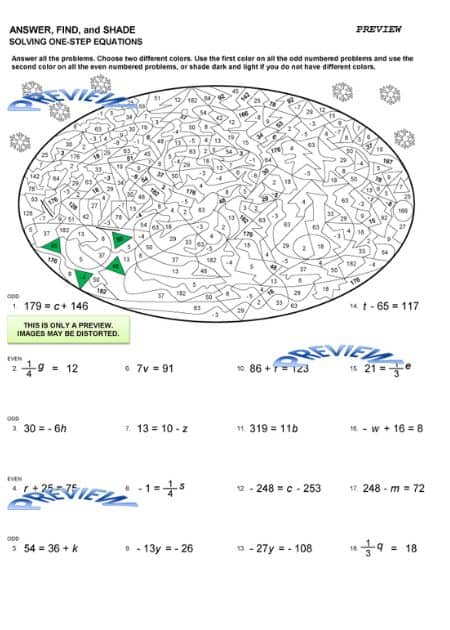
Answer, Find, and Shade Word Sentences and Variables
The below worksheets review verbal sentences and variables. Students read the sentences (equations) and find the missing number.



Solving One-Step Equations Add, Subtract with Decimals
The worksheet covers solving one-step equations with addition and subtraction of decimals. It does not have any negative variables.




Two-Step Fill in the Blanks
The below art worksheets cover solving two-step equations. They help students visualize the process which should lead to solving equation.



Two-Step Equations
The below worksheets cover solving two-step equations.







Percentage
Percentages help us understand an overall account of what is major and minor in a category. Mainly, 100% is kept as the upper limit for easy calculation and understanding.
Percent of Number
Taking 20% of 200. As I mentioned earlier, ‘bracket’ means ‘multiplication,’ so does ‘of.’ Therefore, you can write 20% x 200.
Coming to the actual percentage calculation. There is one long method, and the other is a short method. Understand the one that best suits your way of solving expressions.
The below worksheets describes the percentage problems





Answer, Find, and Shade (2 in 1) Percent of a Number
In the below art worksheets identifies the correct answer and shade it on the given picture. Students need to use their knowledge of percent of numbers to solve various equations.
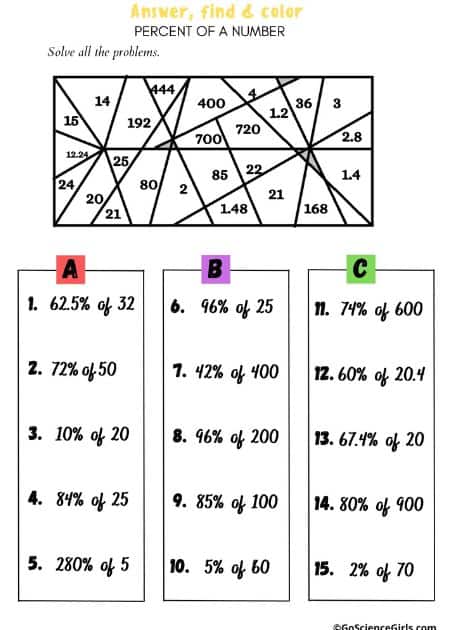
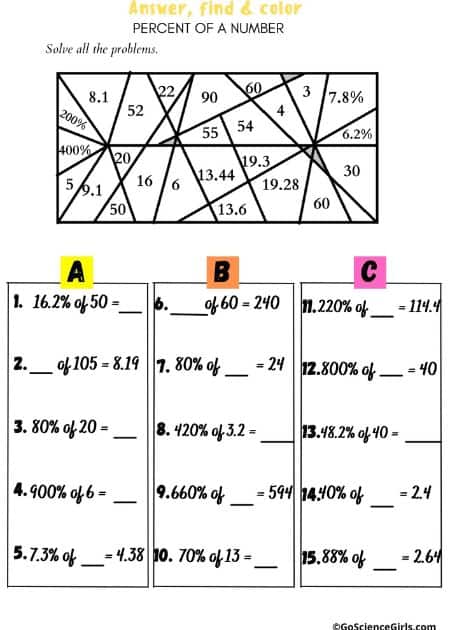
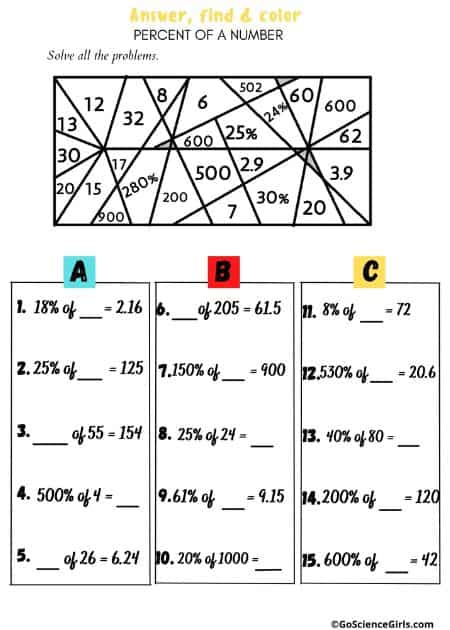

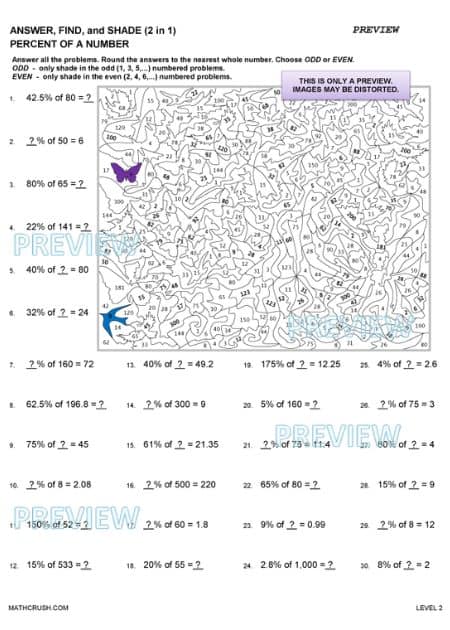
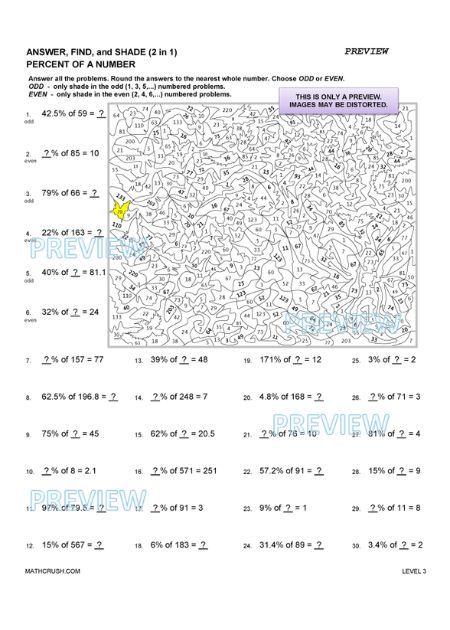
Answer, Find, and Shade Percent of a Number
The below art worksheets review percent of a number. Students need to find the percent of a number, what percent one number is of another, and find the original number when a percent is given.


Long Method –
20% x 200
Remove the percentage sign and write a 100 below the number to be calculated. The numerator is 20, and the denominator is 100 now. 20/100.
Canceling out one zero from above and below, leaving 2/10, that equals ⅕.
Now, the equation has turned out to be 1/5 x 200, which eventually is 200/5. The final answer is 40.
Short Method –
Rather than doing all the above steps, simply place a Decimal point, two members, from left. Always two paces to the left; neither change the direction nor change the pace.
So, 20% x 200 will become 0.20 x 200, that equals 40.
There you have it—both methods for calculating the Percentage.
Some of the most commonly used percentages are 25%, 50%, 75%, and 100%. They are named quarter, half, three-fourth, and full, respectively. Also, their values are 1/4, 1/2, 3/4, and 1.
Note: You can calculate the percentage itself; the percent is given instead of the opposite. To do that, reverse Multiplication with Division, and you will retrace your path to the actual percentage.
Percent of Change
Percentages are rarely constant. Stock markets, profits, losses, share market, etc., are many examples where increases and decreases in various percentages need to be kept track of.
Therefore, it is essential to know how to calculate any decrease or increase in percentages. Here you go –
The formula you need to substitute the values in is –
% increase/decrease = Increase or Decrease / Original x 100.
The increase is the difference between Original and New.
Example : Original – 30, New – 25. Find out the increase.
Solution : Decrease = Original – New
Decrease = 30 – 25
Decrease = 5
% Decrease = Decrease / Original x 100
= 5 / 30 x 100
= 16.66
Therefore, the Decrease in the Percentage is 16.66%, which can also be rounded off to 17%.
There are no sign notations in Percentages. You can know whether there is an Increase or Decrease by comparing the Original and New values.
If the number is negative in the calculation of Increase or Decrease, then it is a decrease. If not, then it is an Increase.
The below art worksheets review percent of change. Students are given an original and new number and must figure out if the change is an increase or decrease and then calculate the percent of change.






Combining Like Terms Art
The below worksheet has students practice combining like terms. It includes using the Distributive Property to simplify the expressions.
Even though a part of an expression or equation is surrounded by parenthesis, it can still be pulled apart using the Distributive Property.

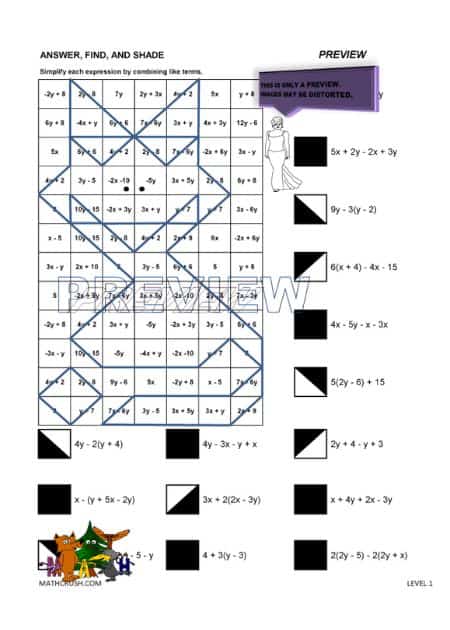
Answer, Find, and Color Multi-Step Equations
The below art worksheets review multi-step equations. worksheets describing how combining like terms, the Distributive Property, and fractions.
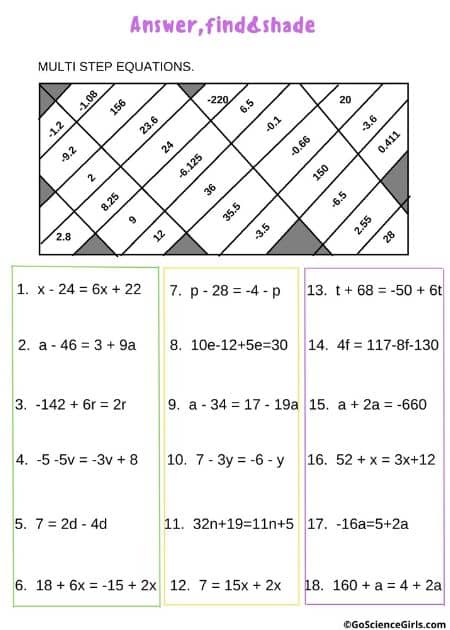
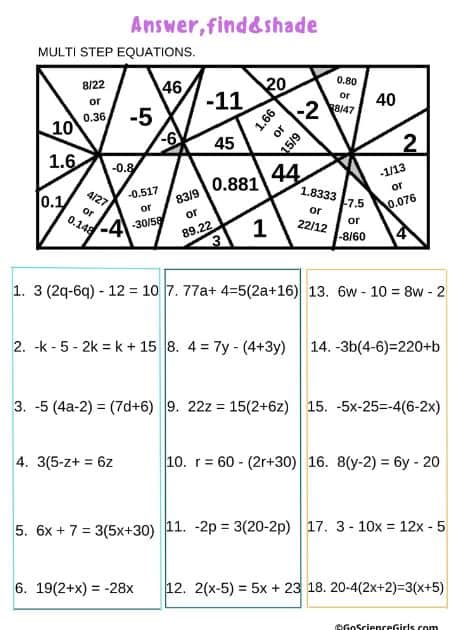
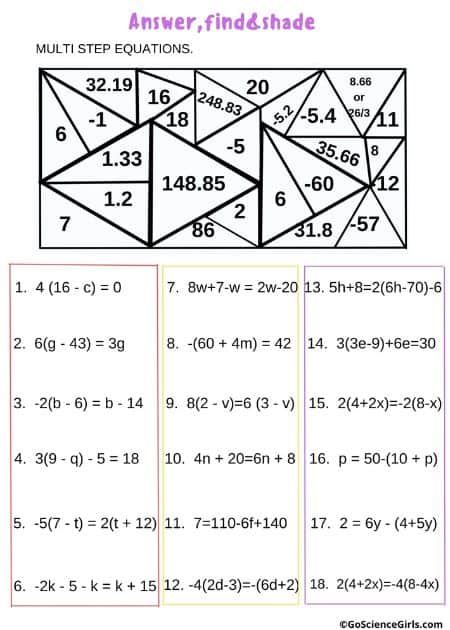

Answer, Find, and Shade Multi-Step Equations
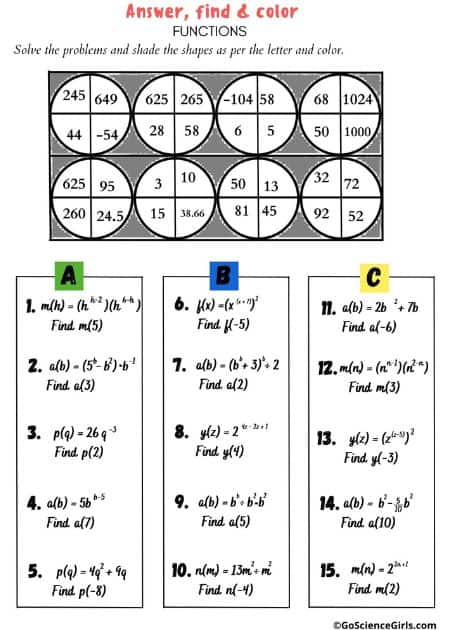
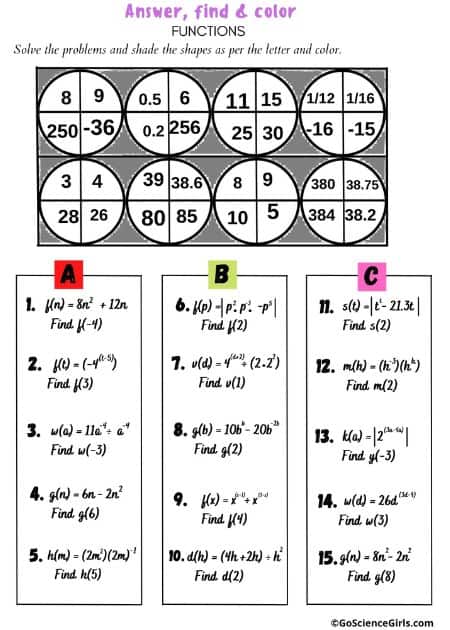
Answer, Find, and Color Functions
The below art worksheets review solving functions. Students need to substitute the given number into the function and solve. The picture and answers are the same but the problems are different for each level.



Multiplying Two Binomials (FOIL)
The below worksheet introduces multiplying two binomials using the FOIL method. It uses the distributive property to help explain the process.
Key concept: The FOIL method helps keep Students organized when multiplying two binomials. FOIL stands for
First-Outer-Inner-Last.

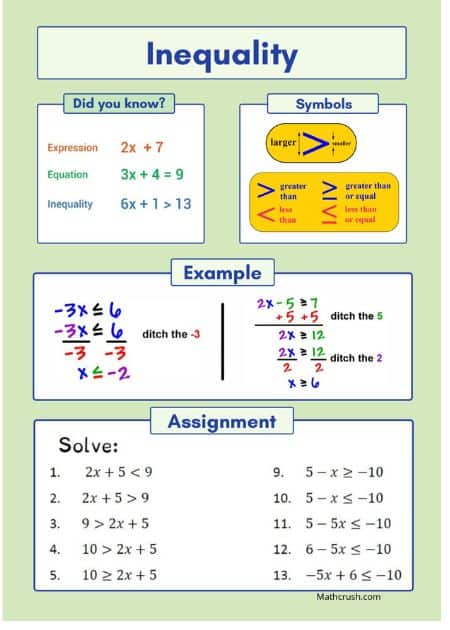
Solving Inequalities
If you come across an Expression with Inequality such as 33p > -2, if you think that you can equalize, or at least reverse the sign of them by multiplying or dividing both sides with a negative number, then you are mistaken.
Let’s prove my point.
Multiply -2 on both sides. You get 33p x -2 and -2 x 2 as -66p and -4.
Therefore, the symbol does not change between them. It remains the same -66p > -4.
The below art worksheet reviews solving inequalities. Students solve two inequalities and find the answer they have in common.

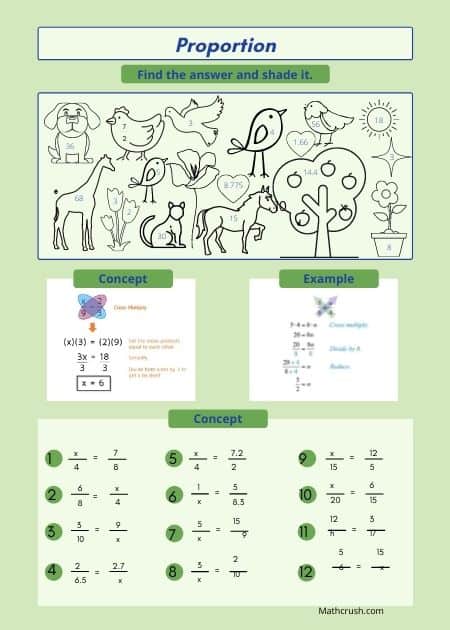
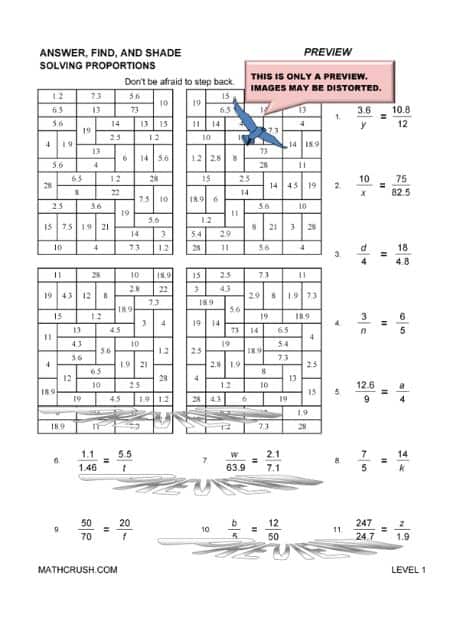
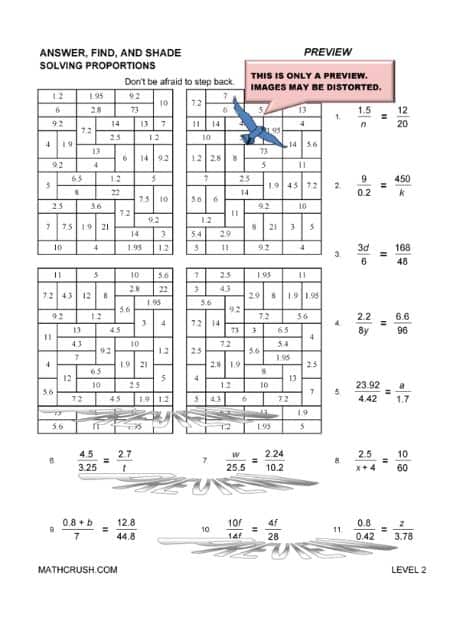
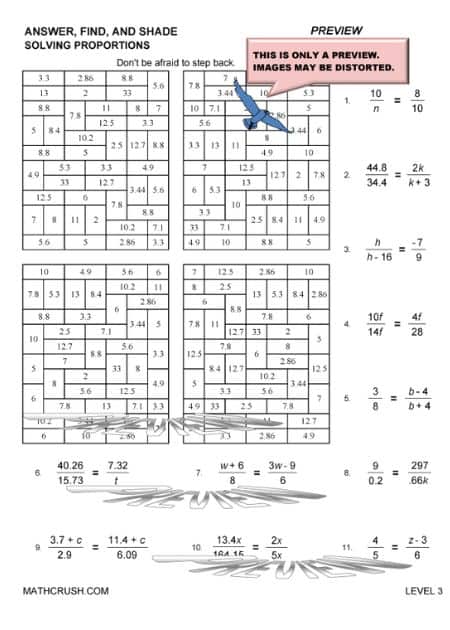
Solving Proportions
Proportions refer to Ratios.
Example : 22/11 = 3/a. Find a.
Solution: Cross multiply the numerator of the left-hand side expression with the denominator of the right-hand side. Similarly, cross multiply the numerator of the right-side expression with the denominator of the left-hand side expression.
You get, 22 x a = 3 x 11
22a = 33
a = 33 / 22
a = 1.5
And this is how you solve proportions.
The below art worksheets review proportions. Students find the missing value in each proportion.


Coordinate Algebra
Algebra has another branch that extends into the graphical representation part of mathematics. And this is called Coordinate Algebra.
Equations and Expressions are formed out of the data being viewed from the graph, and so are the locations calculated and noted from it. The grid view gives exact and precise locations if the scale used to draw the graph has been accurately measured.
Introduction to Coordinates
The Coordinate System is a graphical representation used to locate the position of an object in two-dimensional or three-dimensional spaces. The number line system is used in four extensions from ‘0’ or ‘Origin.’
The right and up number lines are positive, while the left and down number lines are negative. These four lines divide the graph into four quadrants.
The quadrants are marked as roman numbers of I, II, III, and IV, beginning from the upper right corner first, then the one left to it, then the one below it, and the last on the right of the third.
The horizontal line is the ‘x-axis,’ and the vertical line is the ‘y-axis.’ Coordinates are represented within brackets with a comma between the two coordinates: ‘( – 4, 9).’
An object in Quadrant I will have positive coordinates, while in Quadrant III will have negative coordinates. Objects in Quadrants II and IV will have a combination of one positive coordinate and one negative coordinate.
The below video covers coordinates. The video is meant to be used as an introduction or
review video. It introduces coordinates and graphing, and how it is used in the real world. Use the handout as an additional resource for students while they watch the video.
Video:

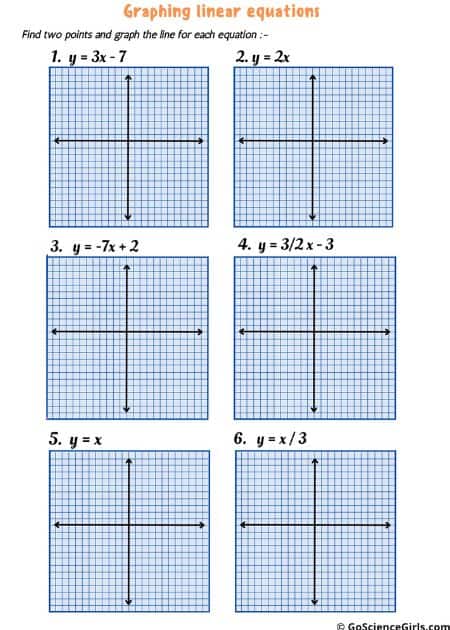
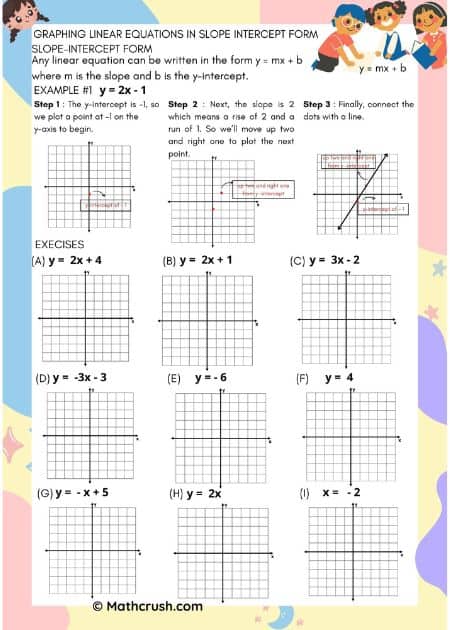
Graphing Linear Equations
To understand how to solve equations using graphs, you will need to go through Graphing Linear Equations.
For each graph, an equation is given. For example, for our comprehension, let us take: 2x – 3y = 5, and the given x values are 3, 4, and 5. Now, what to do about the y values?
Begin by solving the equation using the given three values of the variable x –
2x – 3y = 5
2(3) – 3y = 5
6 – 3y = 5
6 – 5 = 3y
1 = 3y
y = 1/3
2(4) – 3y = 5
8 – 3y = 5
8 – 5 = 3y
3 = 3y
y = 1
2(5) – 3y = 5
10 – 3y = 5
10 – 5 = 3y
5 = 3y
y = 5/3
So, we have the values of x as 3, 4, and 5 from the given data and found the values of y to be 1/3, 1, and 5/3.
Plot the points on the graphs using the coordinates correctly, and you will have the object’s location correctly before you.
In some cases, instead of the x values, y values are given, but you can use the same methodology to find the x values, solve the equation and plot the graph.
The below worksheets cover graphing linear equations. Students find points for each equation and graph the line on the given grid. There is a different worksheet for each level.



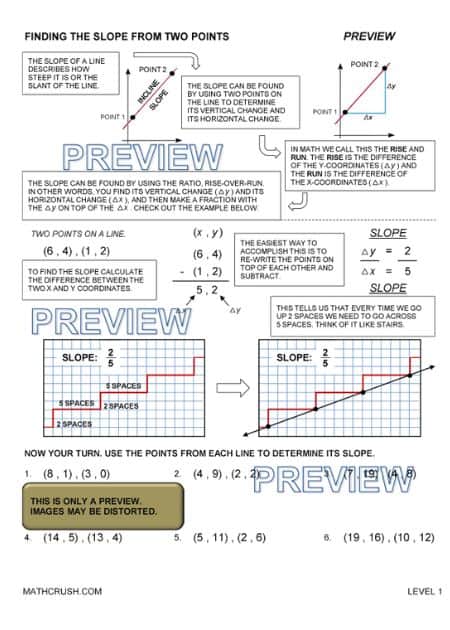
Finding Slope from two points
A slope in a graph defines how slant the line is.
If the consecutive values of coordinates in a graph get closer to 0, then the slope will become increasingly horizontal. And, if those consecutive values are moving farther away from 0, then the slope will get increasingly vertical.
The slope is calculated as the ratio of the difference between two consecutive points on the y-axis to the difference between two successive points on the y-axis.
If the difference of points on the x-axis is 0, which implies that the denominator is 0, then the slope is stated as ‘Undefined.’
Example: Two points given as (4, -3) and (-8, 2)
Solution: Subtract the x coordinates and y coordinates alike. Meaning, subtract -8 from 4, and 2 from -3
-8 – 4 and 2 – (-3)
-12 and 2 + 3
-12 and 5
So, the resulting coordinates are (-12, 5).
Now, for the Slope calculation –
Δy / Δx = Difference in y coordinates / Difference in x coordinates
= 5 / -12





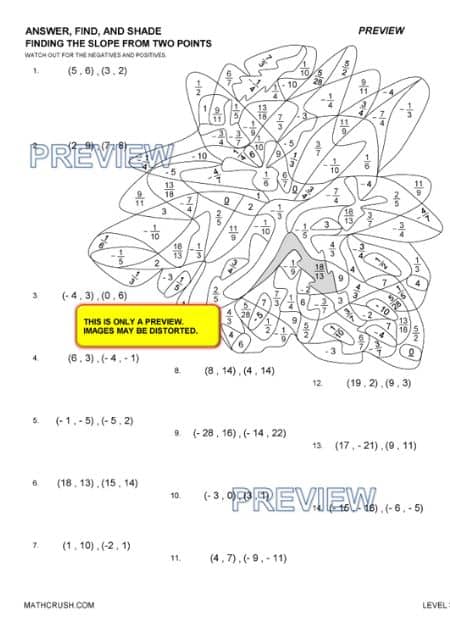
Answer, Find, and Shade Finding the Slope
The below art worksheet reviews finding the slope from two points. Students calculate the slope using the change in x and y.
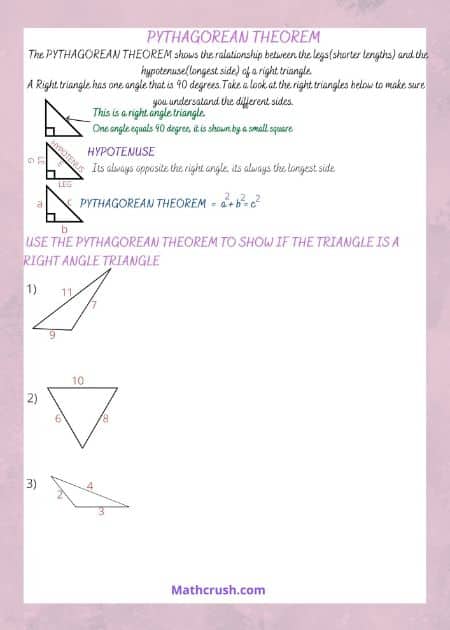
Pythagoras Theorem
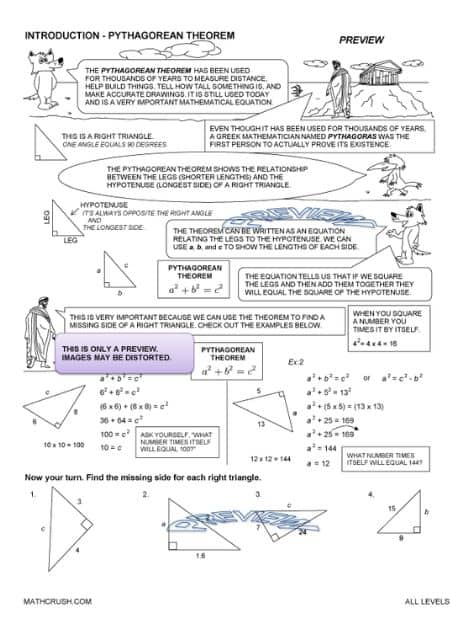
Pythagoras, a Greek Mathematician, is the esteemed owner of the ‘Pythagoras Theorem.’ He proposed the relation of the three sides of a right-angled triangle, meaning a triangle with 90° as one of its angles.
The two legs forming the right angle, denoted by a small square on the inside of the triangle, when squared and added, give the numerical of the remaining one long leg – and this is the statement of Pythagoras Theorem.
Suppose the two short legs as ‘a’ and ‘b,’ and the one long leg also called the ‘hypotenuse’ as ‘c,’ then the expression for the Theorem will be –
c2 = a2 + b2
Remember that this theorem applies only to right-angled triangles. It does not work on scalene, equilateral, or isosceles triangles or any of their variations.
Here is also where you can use your knowledge of squares and square roots to identify the sides of the given right-angled triangle. You will come across both perfect squares and non-perfect squares for many of the right-angled triangles.
In addition to that, if the numbers are big and you face difficulty in their multiplication, you should brush up on your Distributive Property Concept and use it for your problem-solving.
Real-life applications of the Pythagoras Theorem are Construction, Drafting, Measuring Distance, Calculating the height of large objects, etc.
In many cases, only the hypotenuse doesn’t need to be calculated. There are instances where you will need the Theorem to calculate the other sides of the triangle or even half of one side.
Suppose those are the situation, no need to worry. You will have to use the same Theorem, but with a slight rearrangement. Let us look at an example.
Example: The hypotenuse is 16cm, and one short leg measures 2cm. Find the length of the other short arm.
Solution : The theorem is c2 = a2 + b2 right? All you need to do to solve this example problem is rearrange a2 to the left side of the Expression, like this –
c2 – a2 = b2, the sign of a2 changes from positive to negative as the term is shifted not to the left of the same side but to the left-hand side of the entire equation.
The above rearranged equation can also be written as –
b2 = c2 – a2
Substitute the values from the question –
b2 = 162 – 22
b2 = 256 – 4
b2 = 252 or b = √252
This video covers the Pythagorean theorem. It explains what the theorem is and how it can be used. The video includes examples and additional review to help students better understand the theorem and how to use it in everyday life.
Video Link
The below are the worksheets that describes the real world Pythagorean theorem.

Pythagorean Theorem – Level 1
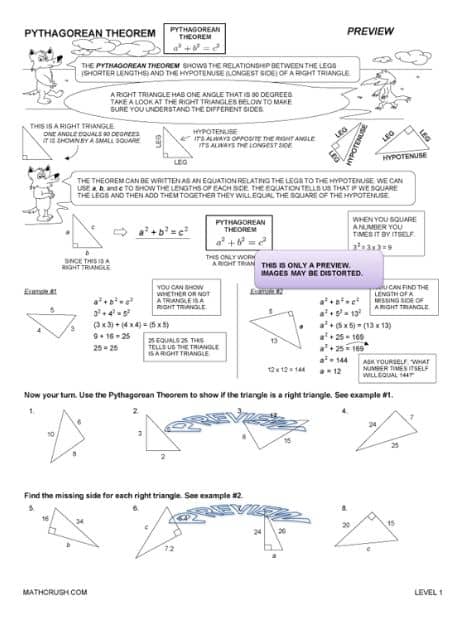
Pythagorean Theorem – Level 2
The below worksheet continues the Pythagorean Theorem.


Pythagorean Theorem – Level 3


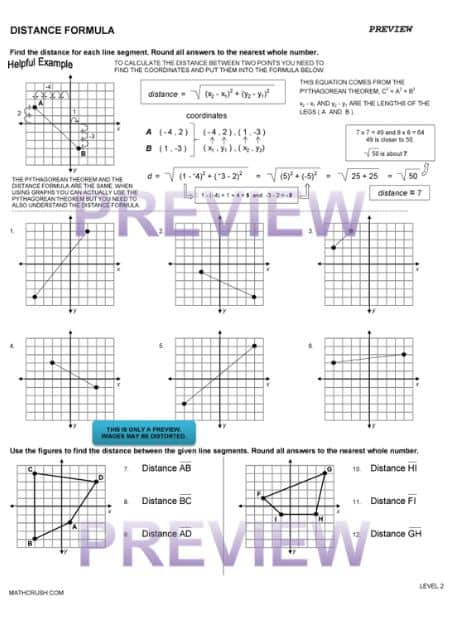
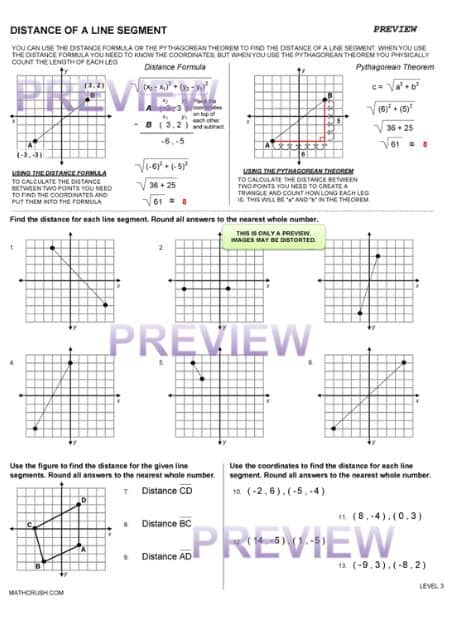
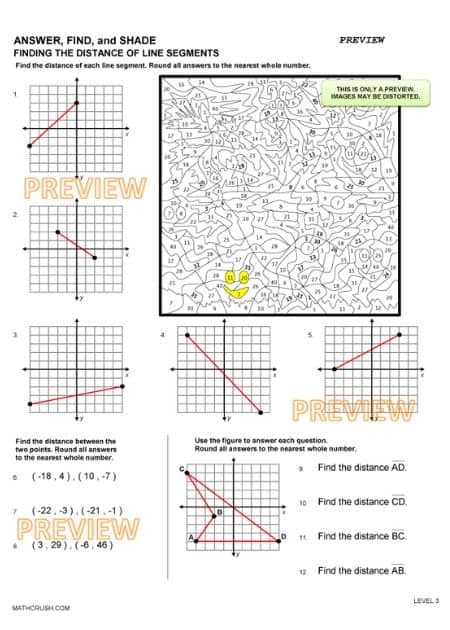
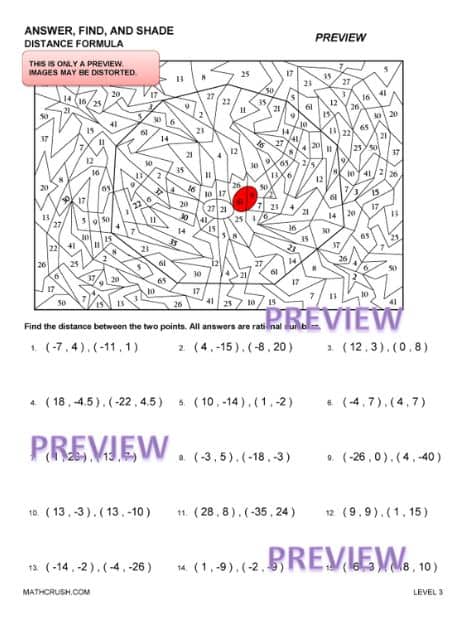
Distance of Line Segments
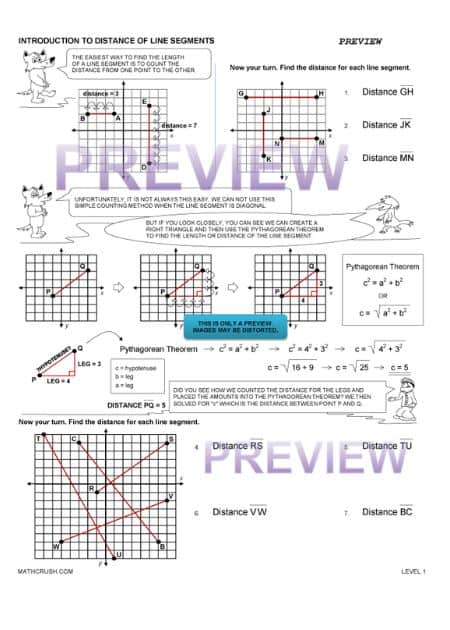
It is easy to measure the distance of the two short arms on a graph as the scale count is whole. But, for the hypotenuse, it is not so easy.
The diagonal line passes through various parts of each grid, sometimes covering one-quarters, and other times a tiny part is left out of the grid, hence using the Pythagoras Theorem to find out its measurement.
A line segment differs from a line as the former has two fixed points, unlike the latter. It has a start point and endpoint, whereas you can extend a line to infinity.
Now, if a line segment is considered and the distance of the said line segment is to be calculated, then the formula used is slightly different from the Pythagoras Theorem. It is –
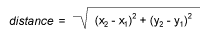
Here, the two x coordinate values ad two y coordinate values are substituted, and distance is calculated. There are possibilities for the answer to arrive at both perfect squares and non-perfect squares.
You can also use this formula to calculate the side measurements of isosceles, scalene, or equilateral triangles and any of their derivatives.
For scalene, you will have to use the formula three times for the three different sides. Isosceles triangle sides require using the formula only twice; once for the two equal sides and once for the third other different side. And, finally, for the equilateral, once is enough as this type of triangle has all its sides equal.
The below worksheet introduces finding the distance of a line segment using a graph. It uses the Pythagorean Theorem to help students better understand how to find the distance.
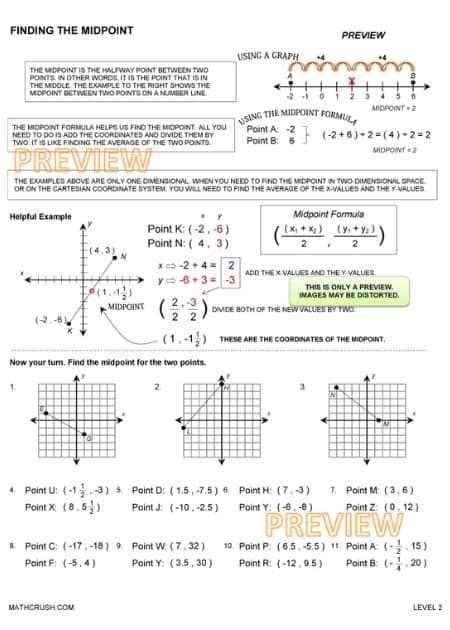
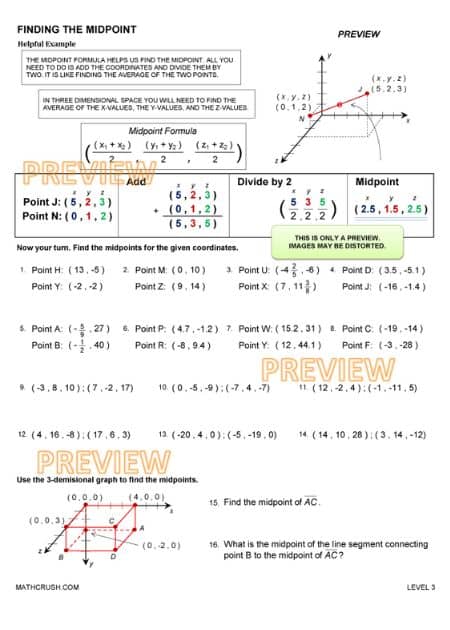
Finding Midpoint
The middle of a line segment is easy if the numbers are small and even in total. But, what do you do to find out the center of the numbers range from 43 and 729?
Hence, a formula has been formulated to help you quickly find the midpoint without worrying much or doing extended mathematical operations where you lose interest halfway through. Here it is –
For two-dimensional midpoint finding –
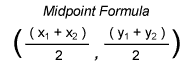
In the formula, the starting and ending coordinates of the x and y axes are taken. Solving both the coordinate sides will give you the mid-point coordinates exactly.
For three-dimensional midpoint finding –
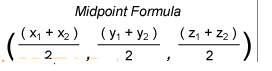
The formula takes the starting and ending coordinates of the x, y, and z axes. Solving the three coordinate sides will give you the mid-point coordinates exactly.
The below worksheet introduces the concept of midpoint and how to find it. It only covers basic number lines.

Algebra – Help Packets
Expressions – Level 1
The below worksheets introduces expressions. It explains what constants, variables, and expressions are and the difference between the three types of expressions (verbal, numerical, and algebraic expressions).
Key concept: Expressions help us connect words to mathematics. Students need to be able to take important information in a word problem and create a mathematical expression to form a solution.


Input – Output Tables – Level 1
The below worksheets introduces input-output tables. It uses pictures to explain the basic concept of the tables. Students complete the tables by drawing pictures and filling in the correct amounts.
Student misunderstanding: The relationship is between the input and output values. Use the fish problem on pages 2 to help explain.Yes, there is a pattern in the output (add 2), but the rule explains the relationship between the input / output numbers.
Commutative and Associative Properties
The below worksheets covers the Commutative and Associative Properties of addition and multiplication. Students learn that the order and groups can be changed, but the final answer will stay the same.
Key concept: Students need to learn that they can move numbers and regroup to make expressions and equations
easier to solve.


Intro to Variables – Level 1
The below worksheet introduces variables to students. It relates the empty box concept
to letters. The problems are designed for mental math and no moving or opposite operations are needed.
Student misunderstanding: Lots of children panic when they see a variable for the first time, but
understand the empty box concept. Use the box as a bridge to variables.


Solving One Step Equations
Add / Subtract – Traditional Method
This below worksheets shows students how to solve one step equations using the opposite
operation method (traditional method).
Student misunderstanding: Equals means the same, and we can alter an equation as long as we
do the exact same thing to both sides.


Solving One Step Equations Add / Subtract – Alternative Method
The below worksheets shows students how to solve one step equations using a method we call the
Arrow Method. It uses the idea that letters and numbers do not get along, and they want to be on opposite sides of the wall (equal sign).
Key concept: Helps students understand which number to move. Ask the question, “Who can we move to make everyone happy?”

Solving One Step Equation– Multiply / Divide
Traditional Method
The below worksheets shows students how to solve one step equations using the opposite
operation method (traditional method).
Student misunderstanding: Equals means the same, and we can alter an equation as long as we
do the exact same thing to both sides.

Solving One Step Equations – Level 1 Multiply / Divide
Alternative Method
The below worksheet shows students how to solve one step equations using a method we call the
Arrow Method. It uses the idea that letters and numbers do not get along, and they want to be on opposite sides of the wall (equal sign).
Key concept: Helps students understand which number to move. Ask the question, “Who can we move to make everyone happy?”

Solving Equations – Additional Help
The below worksheet is designed for students who have a basic knowledge of solving one and two step equations. It is for the students who struggle on which operation to do first and second, and uses a simple tactic to show equations in a different perspective.

Conclusion
These Algebra Worksheets cover all Concepts with a great deal of precision and accuracy. All doubts have been dealt with fluidity and balance.
Going through them with concentration and focus will ease your path further into the world of Algebra, and these foundational steps are the most crucial and vital. Once you gain hold and confidence over these, then you will never have to worry about them in the future one bit.
Good Luck!