Geometry is an early branch of arithmetic studies about spatial relationships concerning specific properties like lines, points, angles, and surfaces. The person who deals with the study of geometrical shapes refers to a geometer. Turn your students, who are interested in the area of geometry into great geometers by letting them practice our interactive geometry worksheets.
Geometry Worksheets for Kids
As the concept of geometry is vast, students need to have good practice of precise sort of worksheet that explains the theory undoubtedly. So, here is the best collection of worksheets that make your student excel in understanding the world of geometry.
Worksheets to Practice Linear Measurements- Answer, Find, and Shade (Level-2)
Linear measures denote the measurement of lengths of various objects using straight-line measurement tools like a ruler, tape measure, etc. In these worksheets, students can calculate the distances of line segments with the help of math equalities and number lines.
Learning Concept: The prior knowledge of number lines makes students master identifying the numbers amid two points on the number lines.

Practice to Basic Skills of Coordinates Worksheets (Video 3)
Coordinates refer to the numbers or letters at particular points on the coordinate plane. These points help students to define the location of geometric elements in a Euclidean space. The video demonstration offers a good review of the coordinates with the help of graphing. Besides, students can also find a few practice handouts that are helpful while solving the problems in the video.
Video

Worksheets that Introduce Polygons Math Concept (Video 2)
The closed plane figure consisting of a set of line segments that do not cross each other but still stay connected refers to the polygon. Forex: Triangles, Quadrilaterals, rectangles, etc. The interactive video demonstration offers step-by-step strategies to familiarize your child with polygons through various activities. Students can have the concept at their fingertips after practicing these fun and easy polygon handouts.
Video

Tangram Activity

Worksheets to Classify Triangles (All Levels)
Triangle is a closed plane polygon with three sides and vertices! Angles take a crucial role to classify triangles into different types such as right-angle triangles, obtuse triangles, etc. The questions in these worksheets help students to master identifying the type of triangle by observing its angles and sides.

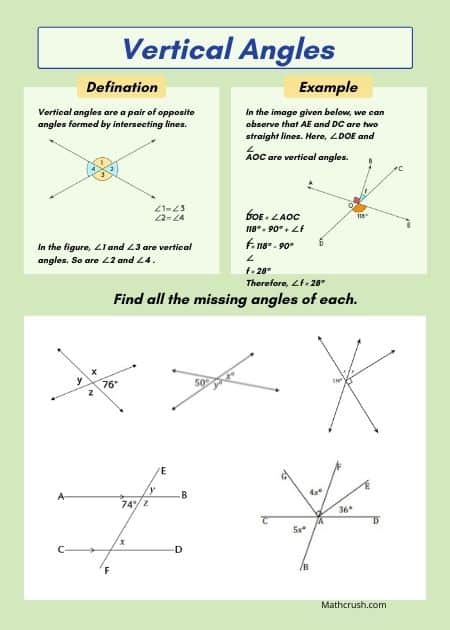
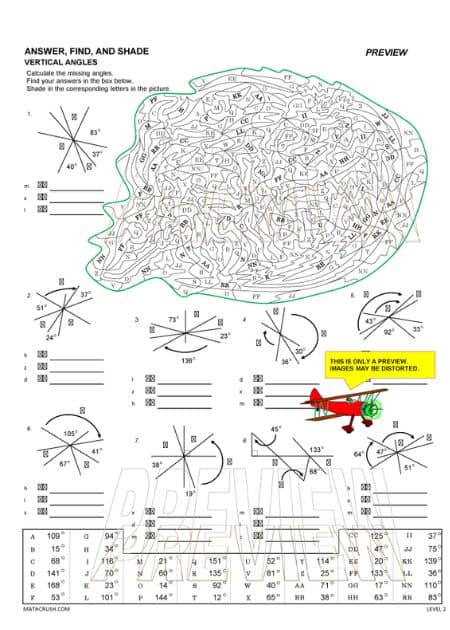
Vertical and Adjacent Angles—Answer, Find, and Shade (Level 2)
The angles that share common vertices and sides denote adjacent angles and the two lines that are opposite and intersect each other refer to vertical angles. Students need to find the missing angles of the questions by identifying the adjacent and vertical angles.
Key Concepts: Students can use the prior knowledge of angles and lines to identify the missing angles that are complementary, supplementary, vertical, etc.
Video Demonstration of Pythagorean Theorem (All Levels)
In geometry, the Pythagorean Theorem is useful for the 2D navigation method. It states that the sum of squares of right-angle sides is equivalent to the square of the hypotenuse side. The worksheets come with a variety of examples and practice activities designed to learn how to use the theorem in daily life. Our worksheets are free and all yours with just a click!
Learning Concepts: Pythagorean Theorem is a significant math concept that comes into use in the field of drafting, construction, and measuring distances.
Learning Tip: Students must have the basic knowledge of square roots and squares to solve the basic problems of triangles.
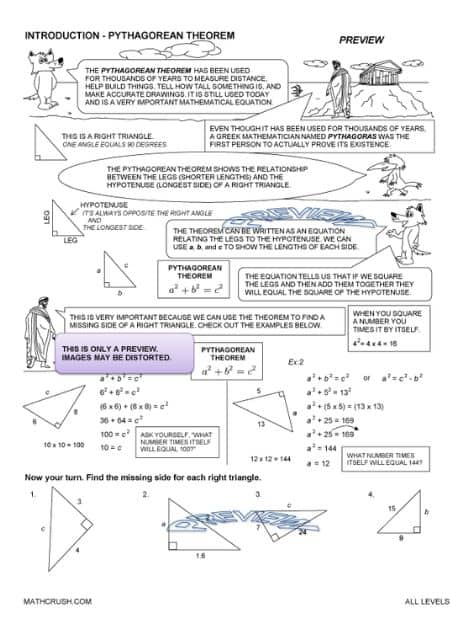
Introduction – Pythagorean Theorem
All Levels
This one page worksheet introduces the Pythagorean Theorem. Students should already know the square and square root of a number, solving basic equations, and triangles.
Key concept: It is a very important theorem in the real world. It is used in construction, drafting, measuring distance, calculating the height of large objects, etc. etc.

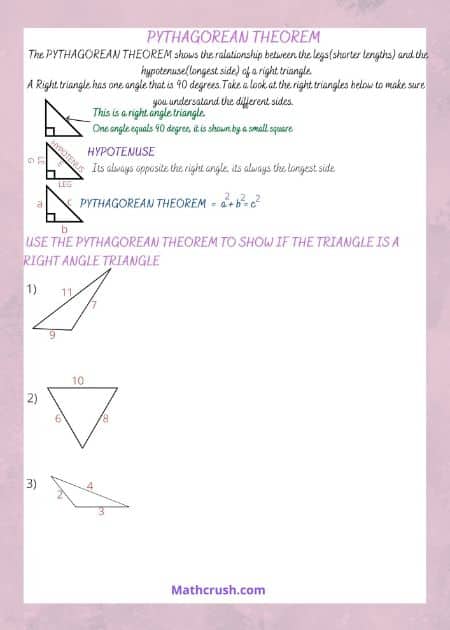
Practice Worksheets of Pythagorean Theorem (Level 1)
The invented right angles through the Pythagorean Theorem are everywhere in the world such as buildings, tables, crystal atomic structures, etc. These worksheets help students to recognize whether the polygons mentioned are right-angle triangles.
Learning Concept: Students can have real-time knowledge of various geometrical shapes in the real world. Besides, the word problems give the required practice of discovering the hypotenuse and leg of a right-angle triangle.
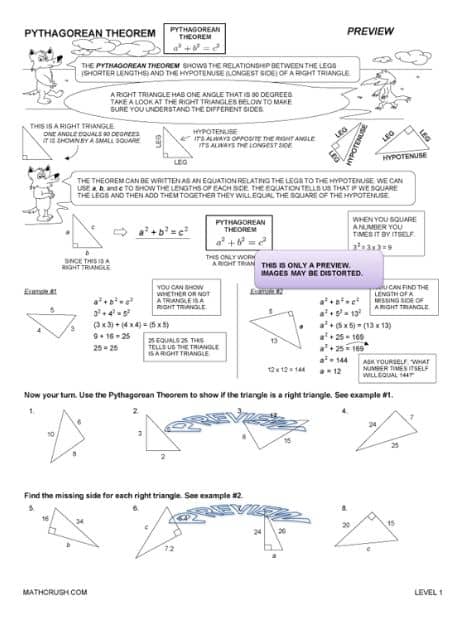
Practice Worksheets of Pythagorean Theorem (Level 2)
The descriptive worksheets allow students to apply the theorem and find out the unknown line segment of a right-angle triangle. However, students must have the basic knowledge of the square roots of irrational and rational numbers.
Helpful Idea: If your student fails to recollect the square root skills, let him review the concepts of estimation square root and estimation irrational numbers.


Practice Worksheets of Pythagorean Theorem (Level 3)
Brighten your child’s knowledge of the Pythagorean Theorem with a variety of word problems that relate to the real world. These problems give a good practice to find the missing side of the right-angle triangle. Besides, they also help in finding the missing side or angle of non-triangular shapes.
Learning Tip: Students must focus on the previous basic knowledge of triangles and the Pythagorean Theorem to solve non-triangular problems.


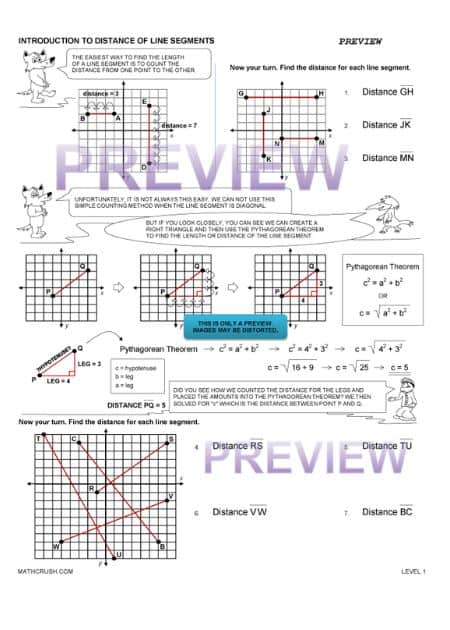
Introduce these Worksheets to Find the Distance of Line Segments (Level 1)
Line segments are the fragments of a line that has definite starting and ending points as well as fixed lengths. The problems will help young learners to understand the methods of measuring the distance of line segments using the Pythagorean Theorem.
Learning Tip: Students must analyze the graphs in the worksheets using the Pythagorean Theorem and apply the distance formula.
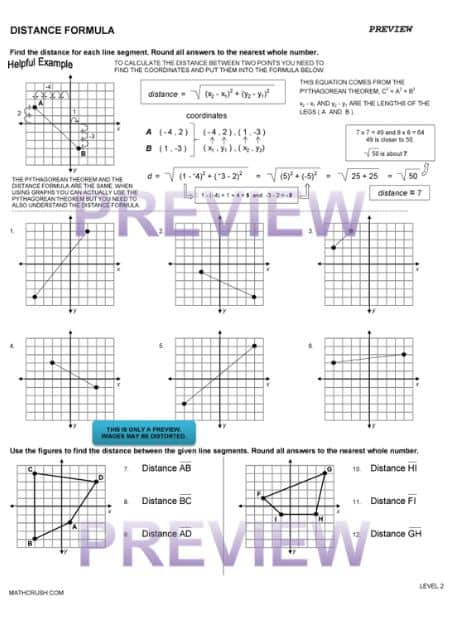
Worksheets to derive Distance Formula (Level 2)
The distance formula is a math principle useful for calculating the distance of a line segment on the line in coordinate geometry. These well-designed worksheets let students have a better understanding and good foundation of the concept in a fun way.
Learning Concepts: The fun learning worksheets make sure that your student can solve real-life problems related to construction.
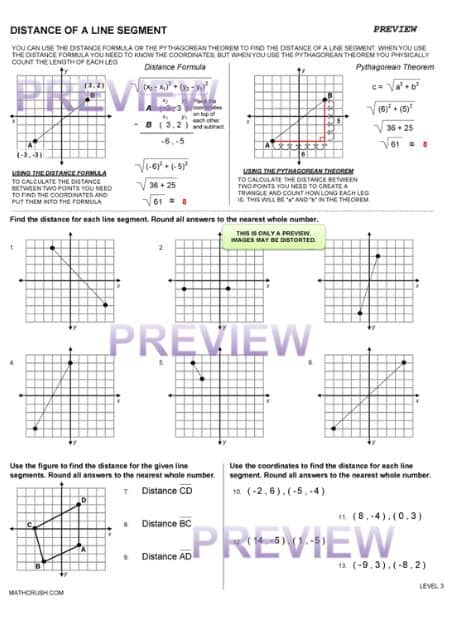
Distance of a Line Segment Worksheets (Level 3)
Develop the problem-solving skills of your students by just practicing these well-structured worksheets designed to find the distance of line segments. These handouts offer the flexibility of learning at the comfort of student’s homes to calculate line segments length with and without graphs.
Learning Concept: Students can relate the differences between the Distance Formula and Pythagorean Theorem after practicing these worksheets.
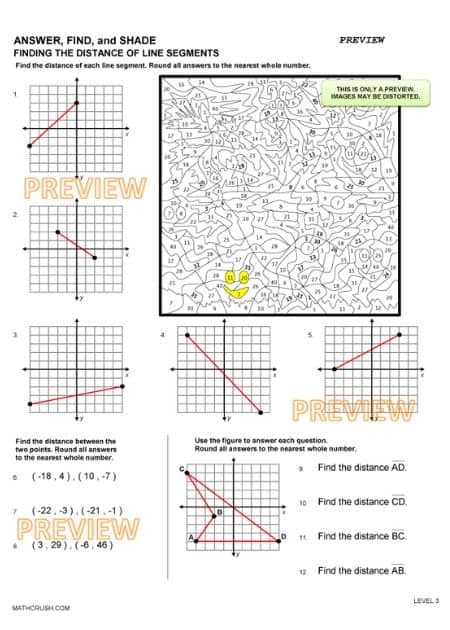
Line Segment Distance Worksheets—Answer, Find, and Shade (Level 3)
Application and rearrangement of variables in the distance formula help measure the distance between two sets of coordinates. Besides, these worksheets provide different strategies that boost the applying skills of formulas to recognize the missing coordinates. On the other hand, applying the Pythagorean Theorem in the distance formula is all that primary school students can do to master coordinate planes.
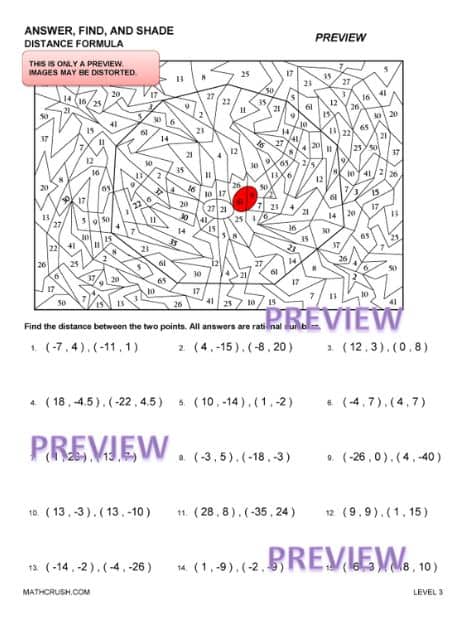
Worksheets to Practice Distance Formula– Answer, Find, and Shade (Level 3)
Find the greatest tool to explore the advanced-level skills of distance formula concerning the Pythagorean Theorem. Yes, these worksheets connect your student to real-world applications by teaching how to substitute x & y coordinates.
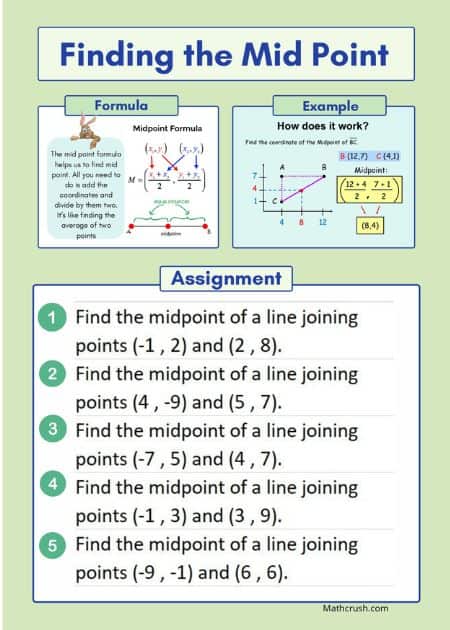
Calculating the Mid-Point Worksheets (Level 1)
The point present at the exact middle position of the line segment and bisecting it into two halves is the mid-point. In geometry, calculating the middle point is useful for analyzing the centroid and median of a triangle. Students can easily calculate the mid-point position by applying the basic skills of number lines.
Previous Knowledge: Before solving the mid-point problems, students need to review the previous knowledge of finding the average among a group of numbers. For the reason that the average and mid-point formulas are equivalent and useful for calculating the average between two numbers.

Calculating the Mid-Point Worksheets (Level 2)
Any sort of line segment consists of only one mid-point, which locates at the equidistant position of two endpoints of it. This section helps the students find well-structured worksheets that cover two-dimensional graphs to find the mid-point.
Learning Concept: Students can plot the two coordinates and calculate their average on the x and y-axis.
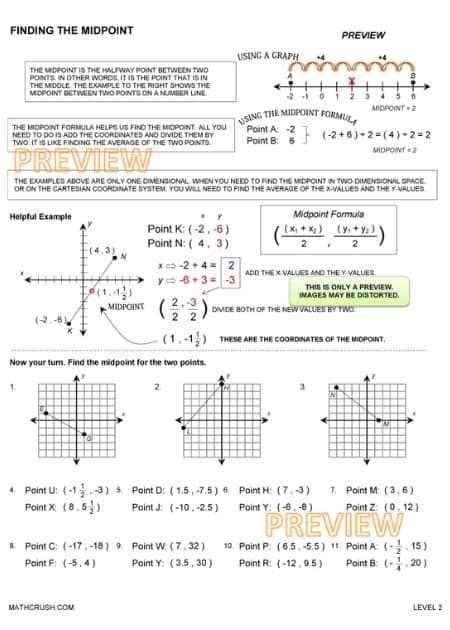
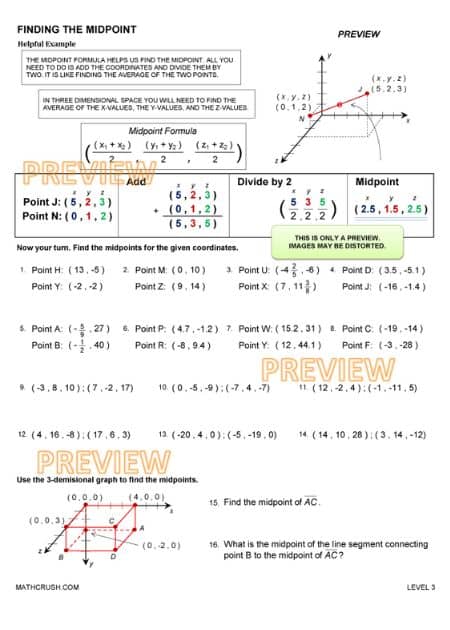
Calculating the Mid-Point Worksheets (Level 3)
These worksheets aid young learners to find the mid-point of a line segment, where its coordinates are in the three-dimensional space. In addition, they also provide 2D and 3D graphs along with the information of two endpoints to find the mid-point.
Previous Knowledge: The learners must have the basic skills of plotting coordinates on the x, y, and z-axis from the previous worksheets. This knowledge helps them to find the mid-point easily and without taking much time.
Game on Geometry– I Have, Who Has? (All Levels)
‘I Have, Who Has?’ is an entertaining game that engages students in learning various geometry terms while having fun. Download the worksheet for free and take as many prints as you want! Later, cut out the squares individually and distribute them to the players (one each). If you have more, you can choose particular students and offer them double. The person who starts the game and the same person is responsible to end the game. So, here is the way one must start the game: the minute the game starter asks the question ‘Who has?’ the other player who has its answer must say, ‘I Have’. And immediately the same person must reveal the question included on the same square. The other player who has the answer for this question must say, ‘I Have’ and reveal the question as well. In this way, the game continues with all the players one by one according to the questions. In the end, the game concludes when the game reaches the first player.
Helpful Idea: Students who are participating in the game must have the geometry terms and concepts at their fingertips. So that, they will not confuse about the game due to a lack of enough knowledge on the concept. Forex: A square is termed a rhombus but a rhombus is not similar to a square.


Worksheets to Practice plotting points on Coordinate plane A
The two-dimensional plane surface formed as a result of the intersection of horizontal and vertical number lines refers to the coordinate plane. Download these worksheets to make students familiarize themselves with plotting ordered pairs on the graph and generate required pictures.
Point to Remember: Students need to learn how to plot a number on the coordinate plane and should be able to identify which number goes first on the x-axis.

Worksheets to Practice plotting points on Coordinate plane B
Practice these worksheets to master recognizing coordinates, ordered pairs, axes, and quadrants. The mystery pictures are hidden in the graph help students to boost their knowledge of identifying ordered pairs.
Learning Tip: Make sure the students are aware of the most significant term of geometry, ‘origin’. Origin is the middle point, where the two lines intersect each other, denoting the value zero at this point.
Worksheets to Practice plotting points on Coordinate plane C
This section of worksheets is useful for learning how to plot the points on the coordinate grid and at the same time how to identify the ordered pairs.
Student Misinterpretation: Students often get confused to identify and plot which number goes first on the coordinate grid. So, they need to have enough knowledge to plot the correct number on the x and y-axis on the coordinate plane.
Worksheets to Practice plotting points on Coordinate plane D
The interactive worksheets consist of coordinate graphs, on which students have to identify the ordered pairs and create a picture.
Student Misinterpretation: Do not confuse the origin with the point of coordinates that meet on the graph. Origin is the starting point on the coordinate plane, whose value is zero because of the intersection of the x and y-axis.
Worksheets to Practice plotting points on Coordinate plane E
The coordinate plane E worksheets teach students how to plot a number on the x and y-axis on the grid. The dependent variable of the question goes on the vertical line (y-axis) but the independent variable goes on the horizontal line (x-axis).
Learning Concepts: The number on the x-axis refers to the x-coordinate and the number on the y axis refers to the y-coordinate.
Worksheets to Practice plotting points on Coordinate plane F
Linear equations are perfect for explaining the dependent and independent variables, which are nothing but x and y coordinates. Here are the worksheets that are easy to edit your choice of variables to plot the coordinates on the graph.
Key Concepts: The graphing representation offers students how the coordinates on the x and y-axis relate to each other to find the solution picture. Every coordinate grid consists of two axes, which are the x and y-axis. The x-axis goes horizontal on the grid but the y axis goes vertical on the grid. The meeting point of these two axes refers to ‘origin’.
Art Worksheets to Practice Line of Symmetry (All Levels)
In geometry, the term line of symmetry refers to the reflected line that divides the shape into two halves. Simply, the line passes exactly in the middle of the shape and the two halves match each other after division.
These worksheets develop the symmetry skills of the students while identifying and drawing a line of symmetry on real objects as well. Besides, they are also perfect for engaging children during Easter events in a fun and educational way.
Learning Concepts: Students learn how to identify the other half of any sort of picture or shape using a line of symmetry skills.




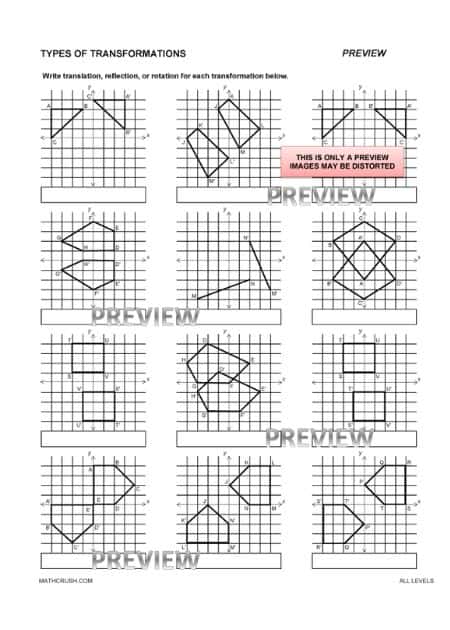
Types of Transformations Worksheets (All Levels)
A transformation in geometry represents the changes in the object rotation on the plane of the coordinate grid. Learn and have a good practice of different types of transformations through our interactive worksheets. They cover three common types of transformations: rotation, reflection, and translation.
Students are asked to identify which type of movement occurred to the object in the coordination grid. Later, they must write the type of transformation as the solution.
Important Concept: There are different types of questions in the form of diagrams. So, students need to guess the object while transformed in each type.

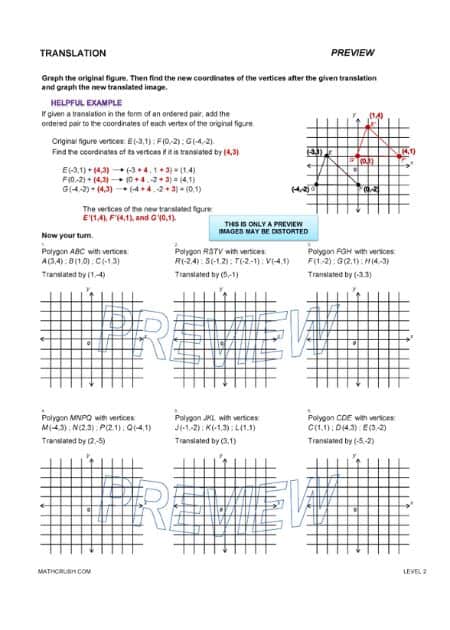
Translation Worksheets (Level 2)
Moving an object in the open area without changing its size, shape, and orientation results in translation type of transformation. Students get the questions on translation with the hints of ordered pair and polygon vertices. Using this data from the question, students need to guess the correct after translation shape of the object.
Learning Tip: Students must be able to recognize the movement occurring in the original shape of the object and later recognize the translation type.
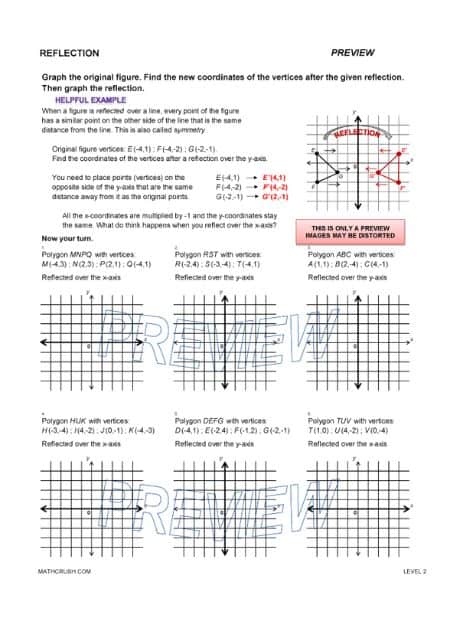
Worksheets on Reflection in Geometry (Level 2)
In geometry and mathematics, reflection is just a “flip”, which means the mirror image of an object or a math expression. Simply, the type of transformation that represents the other equal half of an object or shape using a line of symmetry concept.
The hints of polygon vertices and the reflection of objects represented on the x and y-axis are helpful for students to identify the new reflected shape.
Learning Tip: Observe, identify, and figure out the object shapes and their reflected shapes.
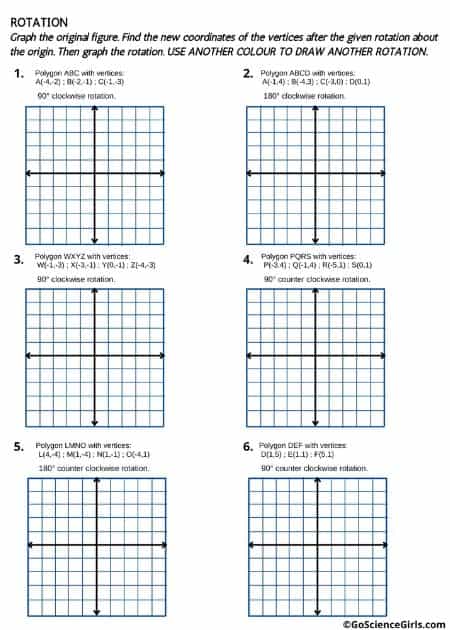
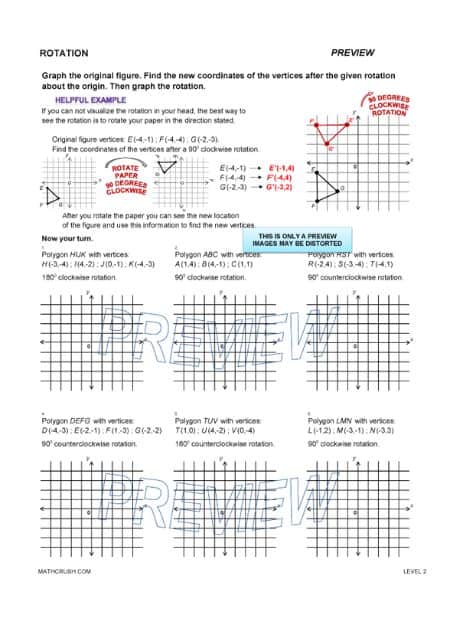
Worksheets on Rotation in Geometry (Level 2)
Rotation is nothing but moving an object without changing its shape and size but fixing it at a standard and immovable point. The rotation of any object around fixed point results in a new shape or picture. To find the new rotated shape or figure, students need to use the information of rotation happening around the origin.
Important Concept: Students can think about, recognize, and figure out the new rotated shape.
Worksheets on Battleship (All Levels)
Battleship is a fun game that keeps students engaged in learning about coordinate planes and Cartesian systems. Each student gets a variety of grids and practice sheets to recognize each player ships location. The main theme of the game is making the students find the location of the opponent’s ships on the grid and solve the problem.
Learning Concept: Students love this fun game while learning about coordinate systems, which tells the horizontal axis is before the vertical axis.


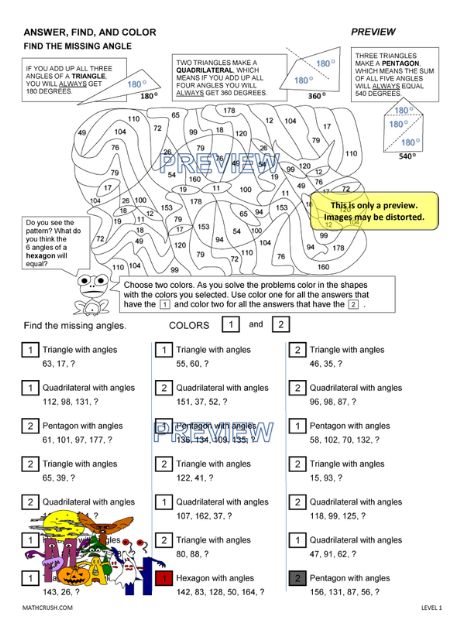
Worksheets on Angle Art (Level 2)
Angle art is nothing but telling the difference between the two intersecting lines! Here are the worksheets that cover pentagons, triangles, hexagons, and quadrilaterals. Students have to figure out the missing angles in these geometrical shapes using colors and shading concepts. The resultant picture shapes are the correct answers for the solutions.
Besides, these worksheets are best for Halloween events to engage students in learning some interesting math concepts.
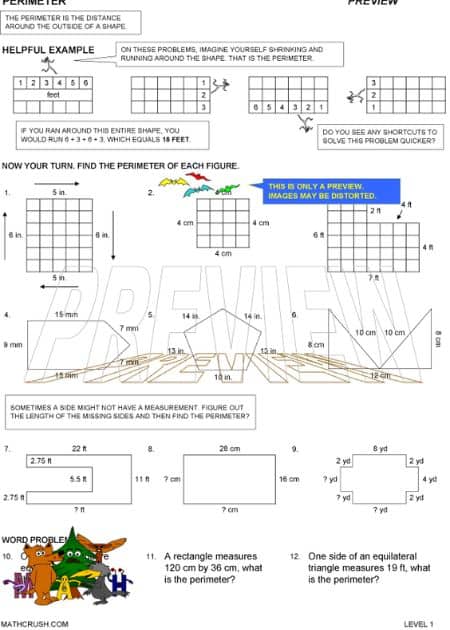
Worksheets to Practice Perimeter Problems (Level 1)
The total distance of a shape around its circumference or boundary or the total length of the path of a 2D shape refers to the perimeter. Get the perimeter skills from these interactive worksheets and excel in finding the perimeter of various geometrical shapes. In addition, check out a choice of activities that help students learn about different 2D shapes.
Misinterpretation of Students: Students often get confused with two significant math concepts: Area and Perimeter. The area is the region present inside the shape or an object whereas the perimeter is the distance around the shape.
Worksheets on Circles (Pi) (All Levels)
A circle is a simple geometrical shape that consists of different points in its plane at a fixed center and radius. Circle worksheets included here cover the problems of calculating circumference, radius, diameter, and area. They are useful as an extension to classroom lessons at home to calculate Pi using a ruler mentioned in these.
Helpful Hint: There are tables to note down the approximate answers that are close to the Pi value. Students have to input their estimated values in these tables and find the correct answers.

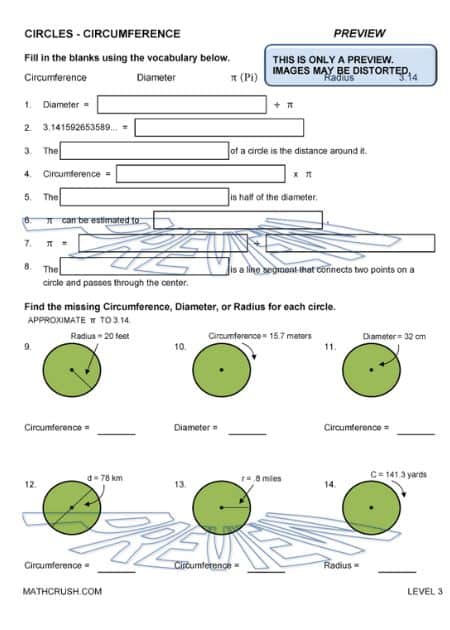
Worksheets to Practice Circles and Circumference
Circumference and circle worksheets use the values of Pi to figure out the diameters and circumferences of circles! In addition, they offer a good practice to relate between diameter and circumference of a circle. Different levels of worksheets offer different levels of difficulty in the questions.
Key Concept: Circumference is nothing but the curved length around the perimeter of a closed figure.



Worksheets to Introduce Area to Students—Video 4
The inside region of two and three-dimensional figures refer to the area and it covers the length and breadth of it as well. The video demonstration on area help students to find out the number of square units and calculate its fractional value on the grid.
Besides, counting and writing the number of square units help students to solve the area problems even if they forget the formulas.
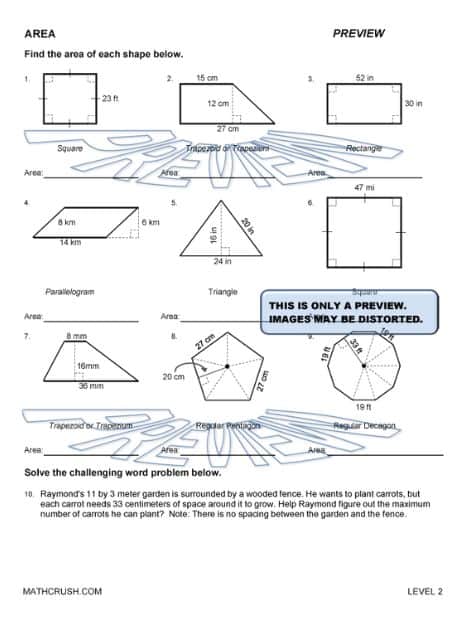
Worksheets to Introduce Area (Level 1)
The area is nothing but the space occupied by a two-dimensional shape in terms of length and width. Square units are the measuring unit of area, like m2, etc. The formula to measure the area of a geometrical shape is a = l × b. Forex: Area of a rectangle with the measurements l = 4cm and b = 5cm is 20cm2
The skill-based worksheets include practice problems on finding the diameter of the circle, area of any sort of geometrical shape. Etc.
Learning Concept: The simple trick of finding area through drawing squares and counting them help students to find out area when they do not remember the formula.


Worksheets to Introduce Area (Level 2)
The prior knowledge of finding area skills in level-1 helps students to solve challenging and interactive word problems on area estimations.
Misinterpretation of Students: To solve these word problems, students need to understand that firstly they have to divide the shapes into polygons.
Worksheets to Practice and Solve Area Puzzle Problems (Level 2)
Area Puzzle worksheets cover simple and easy tricks to figure out whether the given figure is a quadrilateral or not! Learners have to use the information of calculating sides of smaller squares in the shape to determine its shape. Besides, this information helps calculate the length and width of a quadrilateral.
Student Misinterpretation: The calculating devices like rulers, calculators, etc. are just to make calculations easier.


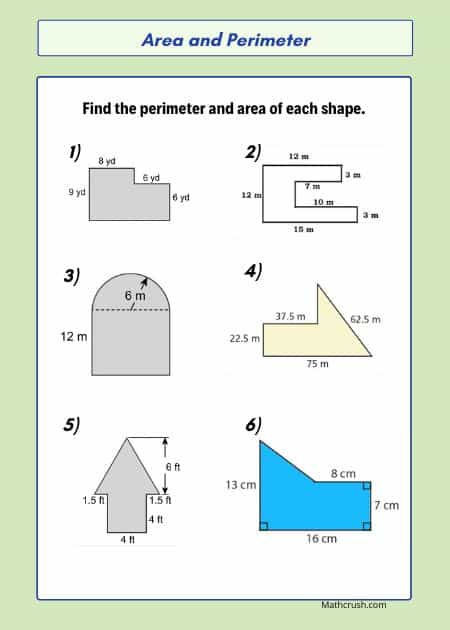
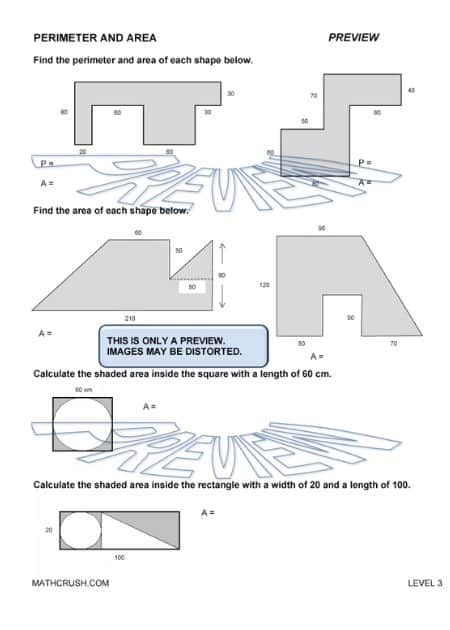
Worksheets to Relate Perimeter with Area (Level 3)
Here are the worksheets that make students introduce the advanced level area and perimeter problems. These problems help them to relate the differences between the perimeter and area math concepts.
Prior Knowledge: Students have to recall the definitions of perimeter and area, which they learned in the introduction worksheets. These basic problems and formulas help them to solve more advanced-level word problems on area and perimeter. Forex: Learning the results of the basic formulas in figuring out the larger shapes into familiarized smaller shapes.
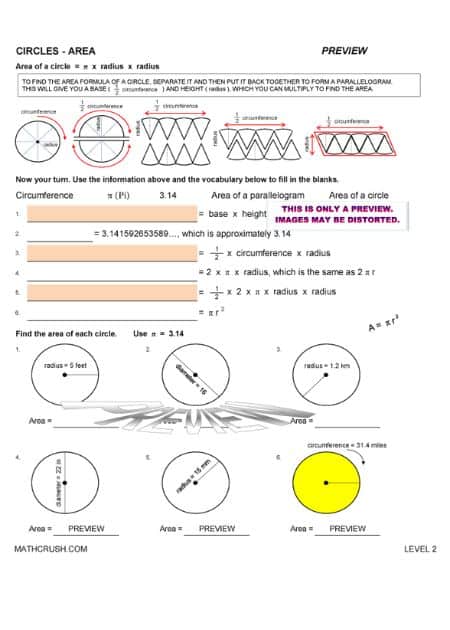
Worksheets to Relate Circles with Area
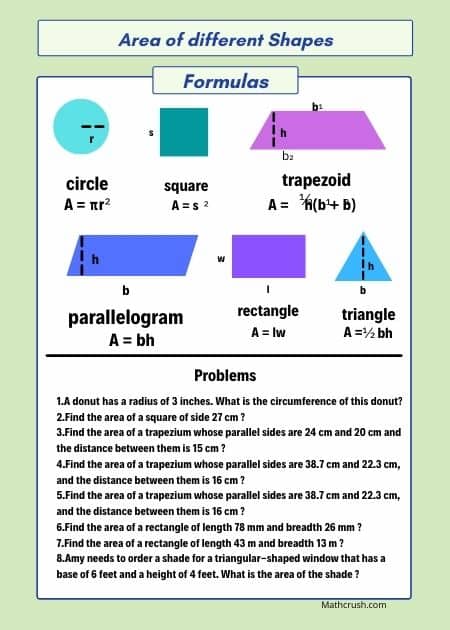
There are three different types of formulas to find the area of a circle, which are: Area = π × r2, where ‘r’ is the radius OR Area = (π/4) × d2, where’d’ is the radius OR Area = C2/4π, where ‘C’ is the circumference. The level 1 worksheets teach students how to determine the formula for finding the area of a circle.


Practice Surface Area Problems Worksheets (Level 1)
The complete area occupied by a solid object around its surface refers to the surface area. The examples and word problems in these interactive worksheets teach how to find the surface area of cubes and prisms.
Learning Tip: In terms of measurements, multiplication of any two measuring units results in the square units. Forex: inches multiplied by inches results in the product in terms of square inches.


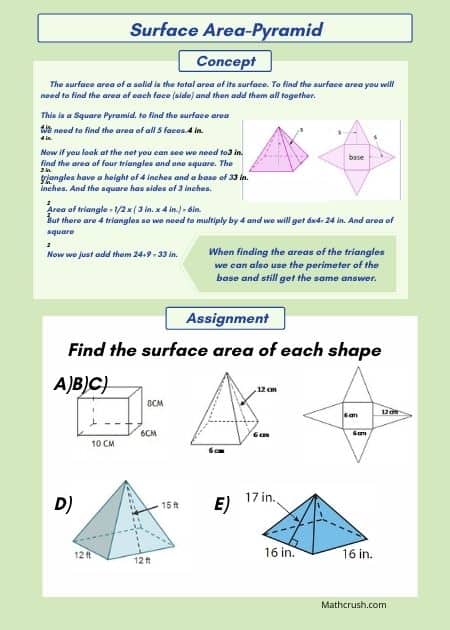
Surface Area of Pyramids Worksheets (Level 2)
Pyramids are three-dimensional figures with a polygon shape as their base and its side meet at a fixed point called vertex or apex. The total sum of the area of base and area of its sides is the surface area of pyramids.
Helpful Idea: Students have to find the area of basic shapes of a polygon.

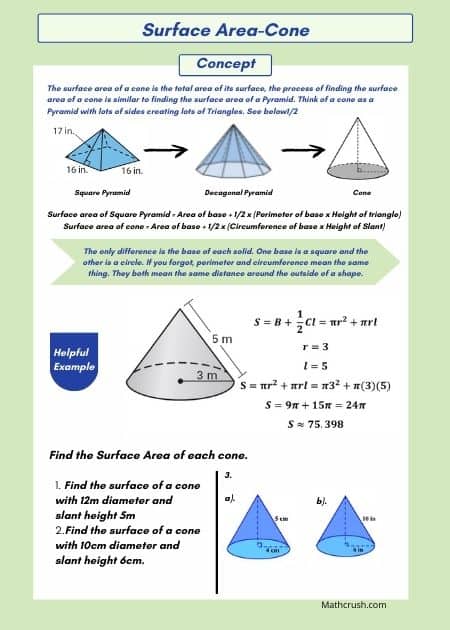
Worksheets to Explain Surface Area of Cones (Level 2)
The 3-dimensional shape with a flat base and an apex at the top, formed with line segments, apex, and points is a cone. The formula to find the surface area of cones is V = πr2 h/3, where r = radius and h = height. The problems in these worksheets help students to relate between surface areas of a cone with a surface area of a pyramid.
Learning Tip: The prior knowledge of the area and perimeter of a circle help to find the surface area of a cone.

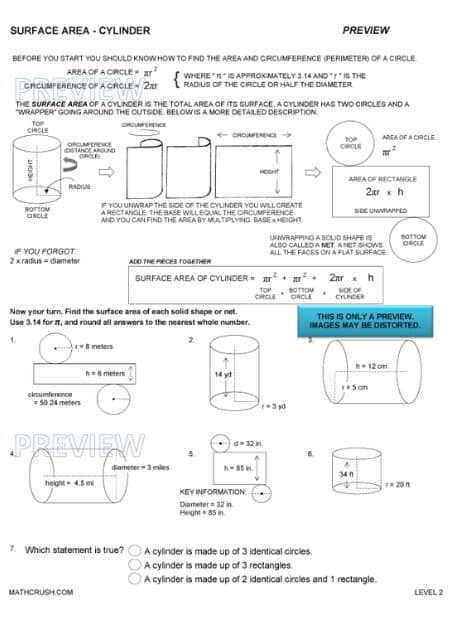
Worksheets to Explain Surface Area of Cylinders (Level 2)
The traditional 3D geometrical shape in the form of a prism with the top and base in the circle shapes is a cylinder. The problems help students to find the simple tricks of calculating the surface area of a cylinder by breaking down its area.
Learning Tip: Learners need to have a thorough knowledge of finding out the inside region and perimeter of a circle to solve the problems.

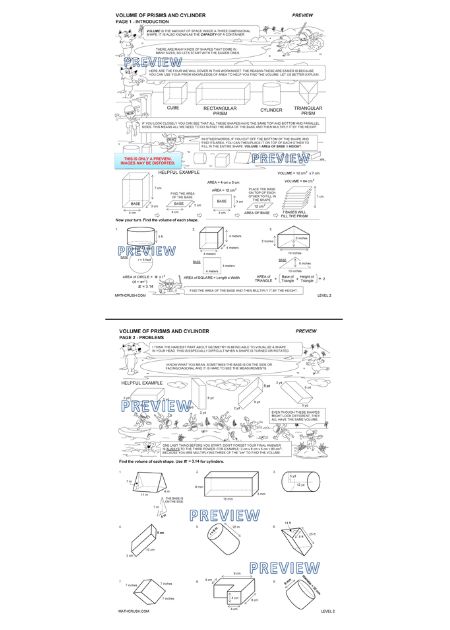
Worksheets on Finding Volume of Cylinders and Prisms (Level 2)
Multiplication of measurements of the area of area and height of a prism results in finding the volume of a prism. Students need to apply the previous knowledge of area and perimeters to find the volume of cylinders and prisms.
Helpful Idea: Square and cubic units are the basic measuring units for calculating the volume of cylinders and prisms.

Worksheets to Relate Volume of Pyramids with Cones (Level 2)
A wide variety of problems to improve the knowledge of geometrical shapes to relate the volume of cones with pyramids.
Additional Resources: Here is the video attachment, which acts as additional help in solving the volume of pyramid and cone shapes. It also tells the relation between the areas of pyramids and prisms in an easier and more fun way.


The volume of Spheres Worksheets (Level 2)
The sphere is nothing but a circle in appearance but it is a three-dimensional sphere in geometry. The worksheets provide simpler forms of equations to understand the concept better. And the word problems are a great source to understand sphere with formula, V=4/3πr3
Additional Source: The video of less duration is interesting with a lot of funny conversations and problems relates to spheres.


Volume Worksheets (Level 2)
Volume is an occupied space of a three-dimensional object or substance in a closed container! Cubic meter is the SI-derived measuring unit that quantifies volume in numbers form. The set of word problems and activities help students how to calculate the volume of various geometrical shapes like cylinders, cones, etc.
Student Misunderstanding: Students often confuse with area and volume as they both sound similar in terms of definition.


Help Page

Geometry Test Ready Worksheets (Level 2)
Explore the wide collection of worksheets that cover a variety of questions in the form of word problems and diagrams. These varieties of questions build a variety of geometrical skills of primary school students. Every question format is designed to test the previous knowledge of geometry. Key Concepts: Pythagorean Theorem, Finding the area and volume of various geometrical shapes, learning about circles, etc. are the key concepts that students learn.

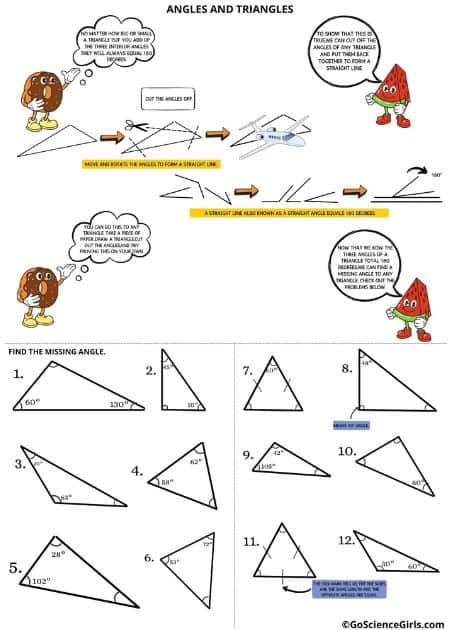
Angles and Triangles – All Levels
This two page help packet helps students better understand the sum of the angles of a triangle. If
you add the three interior angles of any triangle you will get 180 degrees. With this knowledge they are able to find missing angles of triangles.

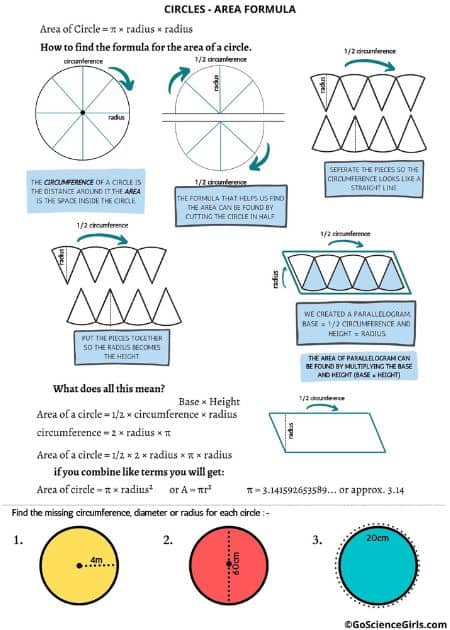
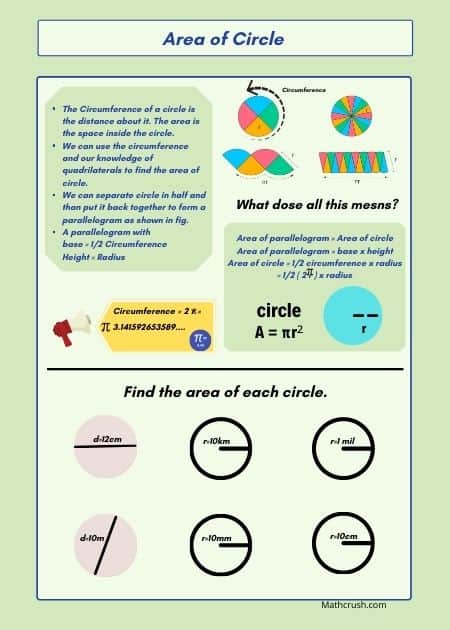
Circles (Area Formula) – All Levels
This one page help worksheet explains where the formula for the area of a circle comes from. It uses pictures to help students relate circles to parallelograms.